要使得二次型为正定的,则t的取值条件是:A. -1B. -1C. t>0D. t
要使得二次型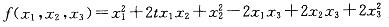 为正定的,则t的取值条件是:
为正定的,则t的取值条件是:
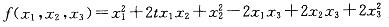 为正定的,则t的取值条件是:
为正定的,则t的取值条件是:
A. -1
B. -1
C. t>0
D. t
B. -1
C. t>0
D. t
参考解析
解析: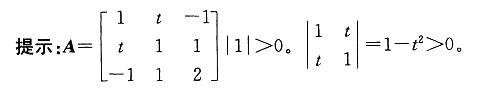


相关考题:
下列说法正确的是().A.任一个二次型的标准形是唯一的B.若两个二次型的标准形相同,则两个二次型对应的矩阵的特征值相同C.若一个二次型的标准形系数中没有负数,则该二次型为正定二次型D.二次型的标准形不唯一,但规范形是唯一的
单选题若矩阵A的各阶顺序主子式均大于零,则该矩阵为()矩阵。A正定B正定二次型C负定D负定二次型