设参数方程 ，确定了y是x的函数，f''(t)存在且不为零，则d2y/dx2的值是：

设参数方程 ，确定了y是x的函数，f''(t)存在且不为零，则d2y/dx2
的值是：

参考解析

解析：提示:利用参数方程求导公式求出dy/dx，在求二阶导数时，先对t求导后，再乘t对x的导数。计算如下：

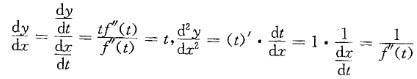
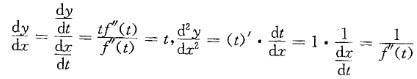
相关考题：

以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
查看答案
设f（x）、f'（x）为已知的连续函数，则微分方程y'+ f'（x）y = f（x）f'（x）的通解是：
查看答案
设参数方程确定了y是x的函数，且f(t)存在，f(0) = 2，f(0) = 2，则当t=0时，dy/dx的值等于：A. 4/3 B. -4/3 C. -2 D. 2
查看答案
设X的分布函数为F(x)=且Y=X^2－1,则E(XY)=_______.
查看答案
设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.
查看答案
设函数z=z(x，y)由方程确定，其中F为可微函数，且F'2≠0，则= A.AxB.zC.-xD.-z
查看答案
已知微分方程y’+y=f(x)，其中f(x)是R上的连续函数.　　(Ⅰ)若f(x)=x，求方程的通解.　　(Ⅱ)若f(x)是周期为T的函数，证明：方程存在唯一的以T为周期的解.
查看答案
设函数y=f(x)由方程确定，则=________.
查看答案
参数方程确定了y是x的函数，且f,(t)存在，f(0) = 2, f,(0) = 2，则当t=0时，dy/dx的值等于（ ）。A. 4/3 B. -4/3 C. -2 D. 2
查看答案
填空题设x2＋xy＋y3＝1，则（d2y/dx2）|x＝1＝____。
查看答案
填空题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。
查看答案
单选题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（　　）。Af″（x）＋f（x）＝0Bf′（x）＋f（x）＝0Cf″（x）＋f′（x）＝0Df″（x）＋f′（x）＋f（x）＝0
查看答案
单选题设确定了函数y＝g（x），则（　　）。Ax＝0是函数y＝g（x）的驻点，且是极大值点Bx＝0是函数y＝g（x）的驻点，且是极小值点Cx＝0不是函数y＝g（x）的驻点D存在x＝0的一个小邻域，y＝g（x）是单调的
查看答案
单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A1/5B1/7C－1/7D－1/5
查看答案
填空题设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。
查看答案
填空题设方程x＝yy确定y是x的函数，则dy＝____。
查看答案
单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A1B－1C1/7D－1/7
查看答案
填空题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为____。
查看答案
单选题设x2＋xy＋y3＝1，则（d2y/dx2）|x＝1＝（　　）。A0B1C2D3
查看答案
填空题函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为____。
查看答案
填空题设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。
查看答案
填空题设函数y＝y（x）由方程y＝1－xey确定，则（dy/dx）|x＝0＝____。
查看答案
单选题设函数y＝f（x）由方程e2x＋y－cos（xy）＝e－1所确定，则曲线y＝f（x）在点（0，1）处的法线方程为（　　）。Ay＋1＝x/2By－1＝x/2Cy＋1＝xDy－1＝x
查看答案
填空题设函数y＝y（x）由方程exy＋ln[y/（x＋1）]＝0所确定，则y′（0）＝____。
查看答案
填空题设函数y＝f（x）由方程e2x＋y－cos（xy）＝e－1所确定，则曲线y＝f（x）在点（0，1）处的法线方程为____。
查看答案
填空题设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝____。
查看答案
单选题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（　　）。Af′（x）＋f（x）＝0Bf′（x）－f（x）＝0Cf″（x）＋f（x）＝0Df″（x）－f（x）＝0
查看答案
热门标签