已知数列{％}的前n项和是 (1)求证：数列{an}是等比数列： (2)记的前n项和Tn的最大值及相应的n值。
已知数列{％}的前n项和是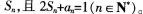 
(1)求证：数列{an}是等比数列：
(2)记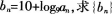
的前n项和Tn的最大值及相应的n值。
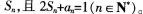
(1)求证：数列{an}是等比数列：
(2)记
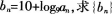的前n项和Tn的最大值及相应的n值。 参考解析
解析：
相关考题：
下面的程序是求菲波那契(Fibonacci)数列的前10项。已知该数列的前两项都为1，即F(1)=1，F(2)=1；而后面各项满足： F(n)=F(n-1)+F(n-2)。请在程序的每条横线处填写一条语句，使程序的功能完整。注意：请勿改动main()主方法和其他已有的语句内容，仅在横线处填入适当的语句。public class Fibonacci{public static void main(String args[]){System.out.printtn("Fibonacci is"+" "+"_______________________);}static long fib(int n){if(______________)return 1;elsereturn _________________}}
已知数列{an}的通项公式为an =(4 9) n-1 - (2 3) n-1 (n ∈ N∗ ),则数列{an}( ).(A)有最大项,没有最小项.(B)有最小项,没有最大项.(C)既有最大项又有最小项.(D)既没有最大项也没有最小项.
已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1．(Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；(Ⅱ)设求证：数列{cn}是等差数列；(Ⅲ)求数列｛an｝的通项公式及前n项和．
已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（ ）A.248B.168C.128D.19E.以上选项均不正确
高中数学《等比数列前n项和》一、考题回顾题目来源：5月19日 上午 重庆市 面试考题试讲题目1.题目：等比数列前n项和2.内容：3.基本要求：(1)引导学生应用等比数列前n项和;(2)试讲10分钟;(3)合理设计板书;(4)要有适当的提问互动环节。答辩题目1.等差数列的前n项和公式是什么?2.怎样才能设计好授课板书呢?你能给出几点建议吗?
已知{an}是由非负整数组成的无穷数列，该数列前n项的最大值记为A。第项之后各(1)若是一个周期为4的数列(即对任意写出dl，dz,d3，d0的值； (2)设d为非负整数，证明：do=一d(n=1，2，3…)的充分必要条件为{an}为公差为d的等差数列： (3)证明：若a1=2，dn=1(n=1，2，3，…)，则{an}的项只能是1或者2，且有无穷多项为l。
在移动平均中，设移动n年则（）。A、当n为偶数时，移动后所得新数列较原数列首尾各缺n∕2项B、当n为奇数时，移动后所得新数列较原数列首尾缺（N-1）∕2项C、当n为偶数时，移动后所得新数列较原数列首尾缺n项D、当n为奇数时，移动后所得新数列较原数列首尾缺n项
单选题已知数列{an}是公差为d的等差数列，Sn是其前n项和，且有S9＜S8＝S7，则下列说法中不正确的是（ ）。AS9＜S10Bd＜0CS7与S8均为Sn的最大值Da8＝0