函数的图像的单调递增区间为__________.
函数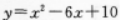
的图像的单调递增区间为__________.
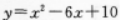的图像的单调递增区间为__________.参考解析
解析：【答案】[3，+∞) 【考情点拨】本题主要考查的知识点为二次函数的单调递增区间．
【应试指导】
由y=χ2-6χ+10=χ2-6x+9+1=(χ-3)2+1，
故图像开口向上，顶点坐标为(3，1)(如图所示）
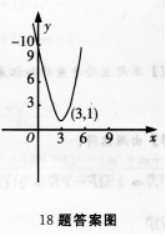
因此函数在[3，+∞)上单调增．
【应试指导】
由y=χ2-6χ+10=χ2-6x+9+1=(χ-3)2+1，
故图像开口向上，顶点坐标为(3，1)(如图所示）
因此函数在[3，+∞)上单调增．
相关考题：
命题p:不经过第一象限的图象所对应的函数一定不是幂函数.命题q:函数y=x+2/x的单调递增区间是[-√2,0)∪[√2,+∞), 则下列命题中,真命题是( ).(A)p∧q.(B)(￢p)∨q.(C)(￢p)∧(￢q).(D)p∧(￢q).
函数单调性是刻画函数变化规律的重要概念,也是函数的一个重要性质。(1)请叙述函数严格单调递增的定义,并结合函数单调性的定义,说明中学数学课程中函数单调性与哪些内容有关(至少列举出两项内容)?(2)请列举至少两种研究函数单调性的方法,并分别简要说明其特点。
函数单调性是刻画函数变化规律的重要概念，也是函数的一个重要性质。（１）请叙述函数严格单调递增的定义，并结合函数单调性的定义，说明中学数学课程中函数单调性与哪些内容有关（至少列举出两项内容）；（７分）（２）请列举至少两种研究函数单调性的方法，并分别简要说明其特点。（８分）
填空题函数y＝x2－lnx2的单调减区间是____。