光滑函数f(χ)的图象如图所示,下列关系式正确的是( )。
光滑函数f(χ)的图象如图所示,下列关系式正确的是( )。 

参考解析
解析: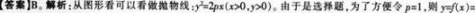

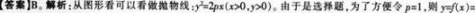

相关考题:
作出函数y=3-2x的图象,根据图象回答下列问题:(1)y的值随着x值增大而__________;(2)图象与x轴的交点坐标是_________________,与y轴的交点坐标是_______________;(3)当x__________时,y>0 。
已知函数f(x)=a2+k的图象经过点(1,7),且其反函数f-1(x)的图像经过点(4,0),则函数f(x)的表达式是 ( )A.f(x)=4x+3B.f(x)=2x+5C.f(x)=5x+2D.f(x)=3x+5
下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4). (1)求出图象与戈轴的交点A,B的坐标; 存在,请说明理由; ° (3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
定义[a,b,c]为函数y=ax2+bc+c的特征数,下面给出特征数为[ 2m ,1-m,-1-m]的函数的一些结论: ①当m=-3时,函数图象的顶点坐标是{1/3,-(8/3)}; ②当m>0时,函数图象截石轴所得的线段长度大于3/2; ③当m1/4时,y随x的增大而减小; ④当m≠0时,函数图象经过同一个点。 其中正确的结论有()。A.②③④B.①②④C.③④D.②④
某教师关于“反比例函数图象”教学过程中的三个步骤为:第一步:复习回顾提出问题:我们已经学过一次函数的哪些内容?是如何研究的?第二步:引入新课。提出问题:反比例函数的图形是什么形状呢?引导学生利用描点法画出y=1/x的图象。列表:描点:连线:引导学生用光滑的曲线连接描点,并用计算机演示图象的生成过程。在此过程中启发学生思考,由于x,y都不能为0,所以函数图象与x轴、y轴不能有交点(如下图)……(第三步过程省略)(1)该教学过程的主要特点是什么?(2)在第二步的连线过程中,如果你是该老师,如何引导学生思考所连的线不是直线,而是光滑曲线(3)对于第三步的③,如果你是该老师,如何引导学生思考函数图象在第一象限(或第三象限)的变化?
问答题若函数f(x,y,z)恒满足关系式f(tx,ty,tz)=tkf(x,y,z)就称为k次齐次函数,验证k次齐次函数满足关系式(其中f存在一阶连续偏导数)x∂f/∂x+y∂f/∂y+z∂f/∂z=kf(x,y,z)。
单选题设f(x)是R上的函数,则下列叙述正确的是()。Af(x)f(-x)是奇函数Bf(x)|f(x)|是奇函数Cf(x)-f(-x)是偶函数Df(x)+f(-x)是偶函数