如图,边长为a的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=________。
如图,边长为a的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=________。
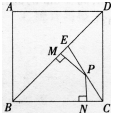

参考解析
解析: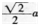
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=
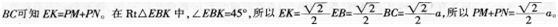
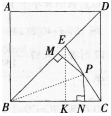
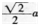
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=
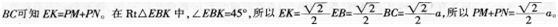

相关考题:
请教:2009年黑龙江省哈尔滨市中考《数学》试卷第2大题第9小题如何解答?【题目描述】18.若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为______________.
设M、N都是自然数,记PM是自然数M的各位数字之和,PN是自然数N的各位数字之和。又记M*N是M除以N的余数。已知M+N=4084,那么(PM+PN)*9的值是( )。A.7B.9C.0D.5
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。 (1)求证:AB为圆的直径; (2)若AC=BD,AB=5,求弦DE的长。
如右图所示,梯形ABCD的对角线AC⊥BD,其中AD=1/2,BC=3,AC=14/5 ,BD=2.1.问梯形ABCD的高AE的值是: A. 43/24B. 1.72C. 42/25D. 1.81
在边长为1的正方形ABCD中,AC与BD相交于O,以A、B、C、D分别为圆心,以对角线长的一半为半径画圆弧与正方形的边相交,如图,则图中阴影部分的面积为多少?(π=3.14)A.0.43 B.0.57C.0.64 D.0.71
下图中ABCD为边长10米的正方形路线,E为AD中点,F为与B相距3米的BC上一点,从E点到F点有小路EGHF,小路的每一段都与AB垂直或平行,且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒,则其以相同速度经EGHF从E点匀速运动到F点用时多少秒?A.12B.10C.9D.8
如右图所示,在△ABC:中,D为AC的中点,E在BC上,且 BE : EC=1 : 2,AE与BD交于F。则△BEF与四边形EFDC 的面积之比为( )。A. 1 : 3 B. 1 : 4C. 1 : 5 D. 1 : 6
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。 A.1B.2C.3D.4
已知BD为正方形ABCD对角线,M为BD上不同于B、D的一个动点,以AB为边在ABCD侧边作等边三角形ABE,以BM为边在BD左侧作等边三角形BMF,连接EF、AM、CM,当AM+BM+CM最短时,∠BCM=( )。A.150B.450C.300D.600
判断题若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上的一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为5/2或12/5。A对B错