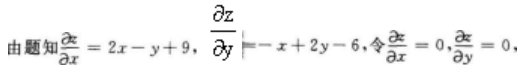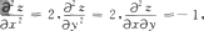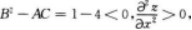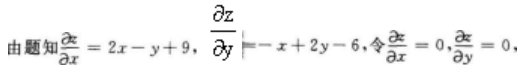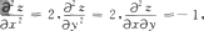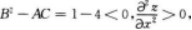设f(x)=xe-x,求函数f(x)的极值(6分)
(本题满分8分) 设函数z=z(x,y)是由方程x+y3+z+e2x=1所确定的隐函数,求dz.
已知(X,Y)服从均匀分布,联合概率密度函数为设Z=max{X,Y}求Z的概率密度函数fz(z)
求函数(x,y)=x2+y2在条件2x+3y=1下的极值.
设函数f(x,y)=X2+Y2+xy+3,求f(x,y)的极值点与极值.
求y=f(x)=2x3-3x2-12x+14的极值点和极值,以及函数曲线的凸凹性区间和拐点.
求函数(x)=x3-3x2-9x+2的单调区间和极值.
对于函数z=xy,原点(0,0)()A.不是函数的驻点B.是驻点不是极值点C.是驻点也是极值点D.无法判定是否为极值点
已知函数(x)=x4-4x+1.(1)求(x)的单调区间和极值;(2)求曲线y=(x)的凹凸区间.
求函数(x,y)=4(x-y)-x2-y2的极值.
设z=z(x,y)是由 确定的函数,求 的极值点和极值
设随机变量(X,Y)的联合密度函数为f(x,y)=(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
设函数z=f(xy,yg(x)),其中函数f具有二阶连续偏导数,函数g(x)可导且在x=1处取得极值g(1)=1.求
设函数(I)求f(χ)的单调区间;(Ⅱ)求f(χ)的极值.
设Z=Z(x,Y)是由方程x+y3+z+e2=1确定的函数,求dz
求函数一的单调区间、极值及其曲线的凹凸区间和拐点.
设二元函数z=xy,则点Po(0,0)()A.为z的驻点,但不为极值点B.为z的驻点,且为极大值点C.为z的驻点,且为极小值点D.不为z的驻点,也不为极值点
线性规划问题是针对()求极值问题。A、约束B、决策变量C、秩D、目标函数
线性规划问题是求极值问题,这是针对()A、约束B、决策变量C、秩D、目标函数
约束条件是求目标函数极值时的某些限制,一般指原料、人力、设备、经费、时间等方面的限制。
问答题求由方程x2+y2+z2-xz-yz-2x-2y+2z-6=0确定的函数z=z(x,y)的极值。