已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．
由曲线y=x3，y=0，x=－1，x=l所围图形的面积为____。
求由曲线y=ex，y=e-x及x=1所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积Vx.
已知t0．05／2,18—2．101，则区间（2．101—2．101)与曲线所围面积是
在区间[0，2π]上，曲线：y=sinx与y=cosx之间所围图形的面积是：
求曲线y=，直线z=1和z轴所围成的有界平面图形的面积s，及该平面图形绕2轴旋转一周所得旋转体的体积V．
求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积．
已知曲线C为y=2x2及直线L为y=4x．①求由曲线C与直线L所围成的平面图形的面积S；②求曲线C的平行于直线L的切线方程．
已知函数(x)=-x2+2x．①求曲线y=(x)与x轴所围成的平面图形面积S；②求①的平面图形绕x轴旋转一周所得旋转体体积Vx．
①求由曲线y=x，y=1/x，x=2与y=0所围成的平面图形的面积S；②求①中的平面图形绕x轴旋转一周所得旋转体的体积V．
设D为曲线y=1-x2，直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·①求平面图形的面积；②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．
①求曲线y=ex及直线x=1，x=0，y=0所围成的图形D的面积S：②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．
①求在区间(0，π)上的曲线y=sinx与x轴所围成图形的面积S；②求①中的平面图形绕x轴旋转一周所得旋转体的体积Vx．
设D是由曲线与围成的平面区域，求D绕x轴转一周所得转体的体积和表面积.
求直线 绕 轴旋转一周的旋转曲面的方程，并求该曲面与平面所围立体的体积。
设曲线L的方程为 ， （I）求L的弧长； （II）设D是由曲线L，直线x=1，x=e及x轴所围平面图形，求D的形心的横坐标
设非负函数满足微分方程，当曲线过原点时，其与直线x=1及y=0围成平面区域D的面积为2，求D绕y轴旋转所得旋转体的体积
(1)求f(x)和g(x)围成的平面区域的面积.?(2)求0≤y≤f(x), 1≤x≤3,绕y轴旋转的体积.?
设曲线及x=0所围成的平面图形为D．(1)求平面图形D的面积s．(2)求平面图形D绕y轴旋转一周生成的旋转体体积V
求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积·
(1)求曲线y=f(x)；(2)求由曲线y=f(x)，y=0，x=1所围图形绕x轴旋转一周所得旋转体体积．
(1)求曲线Y=ex及直线x=1，x=0,y=0所围成的平面图形(如图3—3所示)的面积A．(2)求(1)中平面图形绕x轴旋转一周所得旋转体的体积Vx.
在XOY坐标系下，在[a，b]中曲线y=f（x）始终在曲线y=g（x）之上，则由它们所围平面区域的面积为：f（x）―g（x）在[a，b]上的定积分。
判断题在XOY坐标系下，在[a，b]中曲线y=f（x）始终在曲线y=g（x）之上，则由它们所围平面区域的面积为：f（x）―g（x）在[a，b]上的定积分。A对B错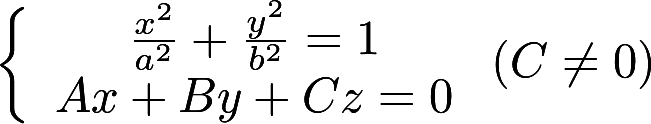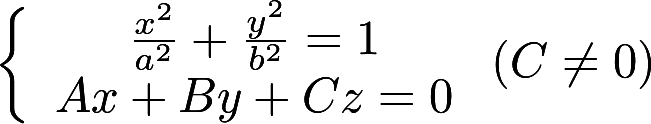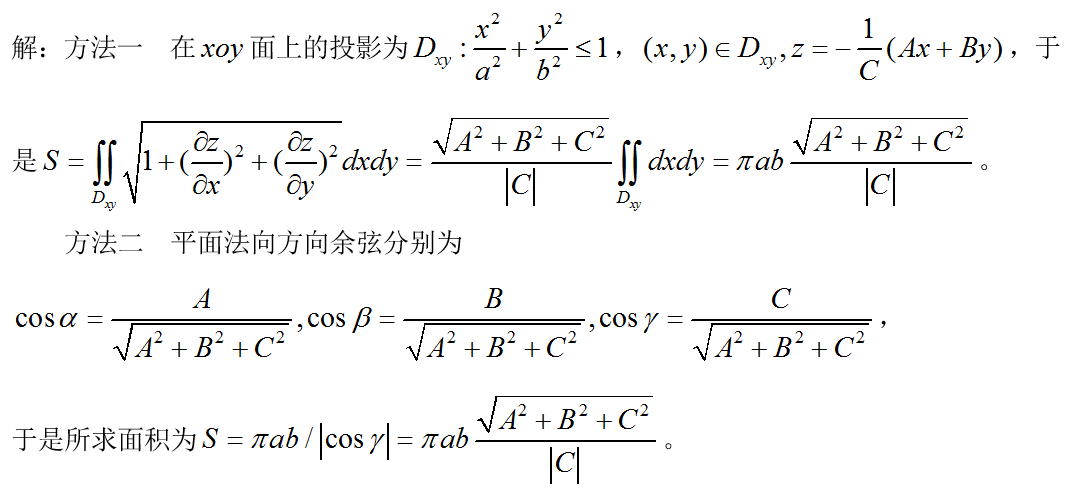
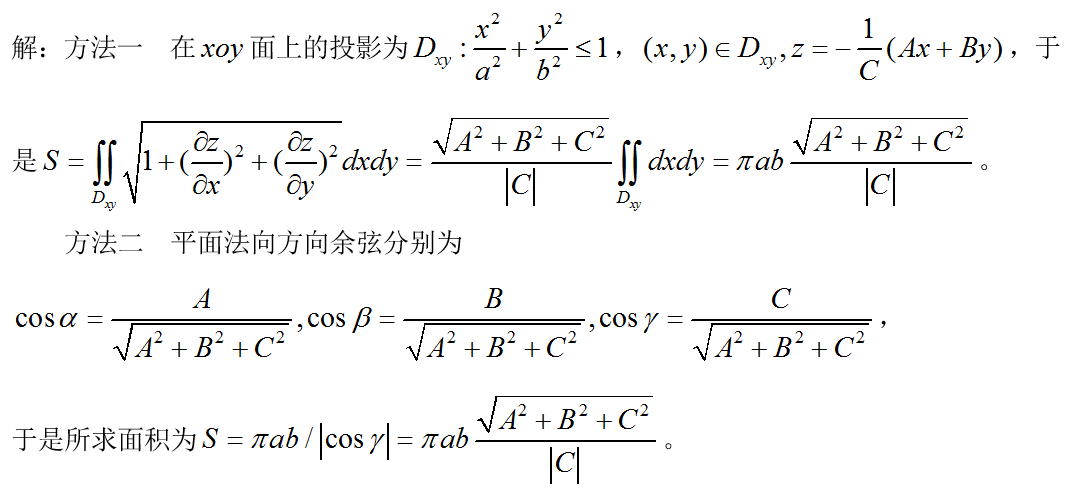
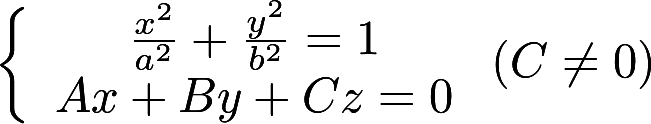所围平面区域的面积。