如果实对称矩阵A与矩阵合同，则二次型xTAx的规范形为().A.B.C.D.
下列说法正确的是().A.任一个二次型的标准形是唯一的B.若两个二次型的标准形相同,则两个二次型对应的矩阵的特征值相同C.若一个二次型的标准形系数中没有负数,则该二次型为正定二次型D.二次型的标准形不唯一,但规范形是唯一的
实二次型矩阵A正定的充分必要条件是（ ）。A.二次型的标准形的n个系数全为正B.|A|＞0C.矩阵A的特征值为2D.r（A）=n
设二次型当 λ 为何值时，f是正定的？A.λ>1B.λ>2C.λ>2D.λ>0
矩阵所对应的二次型的标准形是（ ）。 A． f＝y1^2－3y2^2 B． f＝y1^2－2y2^2 C． f＝y1^2＋2y2^2 D． f＝y1^2－y2^2
设二次型要使f的秩为2，则参数t的值等于（ ）。A．3B．2C．1D．0
设二次型. （Ⅰ）求二次型的矩阵的所有特征值； （Ⅱ）若二次型的规范形为，求的值
设二次型 (b>0), 其中二次型的矩阵A的特征值之和为1，特征值之积为-12. (1)求a，b的值； (2)利用正交变换将二次型f化为标准形，并写出所用的正交变换和对应的正交矩阵.
已知二次型的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解
已知二次型经过正交变换化为标准型，求参数a,b及所用的正交变换矩阵
设二次型,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化为标准型
二次型, (1)求f(x1,x2,x3)的矩阵的特征值. (2)设f(x1,x2,x3)的规范形为. 求a
设二次型其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型化成标准型(需写出正交变换及标准型)
设二次型f(x1,x2,x3)=（a>0）的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.
已知，二次型的秩为2. （Ⅰ）求实数a的值； （Ⅱ）求正交变换将二次型化为标准型
已知二次型f(x1，x2，3x)=x^TAx在正交变换x=Qy下的标准形为，且Q的第3列为. (Ⅰ)求矩阵A； (Ⅱ)证明A+E为正定矩阵，其中E为三阶单位矩阵.
设二次型的正惯性指数p=2,负惯性指数q=0,且可用可逆线性变换x=Cy将其化为二次型（1）求常数a; (2）求可逆线性变换矩阵C
三阶矩阵 为矩阵A的转置，已知r(ATA)=2，且二次型(1)求a； (2)求二次型对应的二次矩阵，并将二次型化为标准型，写出正交变换过程。
设二次型f(x1,x2,x3)在正交变换为x=py下的标准形为若Q=(e1-e3，e2)，则f(x1,x2,x3)在正交变换x=Qy下的标准型为( )。A．B．C．D．
二次型f(x1,x2,x3)=(λ-1)x12+λx22+(λ+1)x32,当满足（ ）时，是正定二次型。 A. λ>-1 B. λ>0 C. λ>1 D. λ≥1
若矩阵A的各阶顺序主子式均大于零，则该矩阵为（）矩阵。A、正定B、正定二次型C、负定D、负定二次型
已知5阶对称阵A的特征值为-1，0，0，1，1，则二次型f=xTAx的秩等于（）．A、1B、3C、4D、5
单选题已知5阶对称阵A的特征值为-1，0，0，1，1，则二次型f=xTAx的秩等于（）．A1B3C4D5
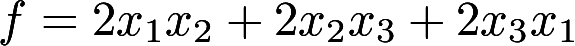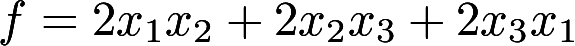, (1)求出二次型f 的矩阵A的特征值;(2)写出二次型f 的标准形。