设二次型f(x1,x2,x3)在正交变换为x=py下的标准形为若Q=(e1-e3，e2)，则f(x1,x2,x3)在正交变换x=Qy下的标准型为( )。A．B．C．D．
设二次型f(x1,x2,x3)在正交变换为x=py下的标准形为
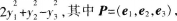若Q=(e1-e3，e2)，则f(x1,x2,x3)在正交变换x=Qy下的标准型为( )。
A．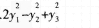
B．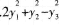
C．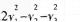
D．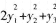
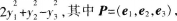若Q=(e1-e3，e2)，则f(x1,x2,x3)在正交变换x=Qy下的标准型为( )。
A．
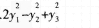
B．
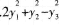
C．
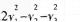
D．
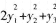
参考解析
解析：
相关考题：
对于三端式振荡器,三极管各电极问接电抗元件X(电容或电感),C、E电极问接电抗元件X1,B.E电极间接X2.C.B电极问接X3,满足振荡的原则是()。 A、X2与X3性质相同，X2、X3与X1性质相反B、X1与X2、X3性质均相同C、X1与X3性质相同，X1、X3与X2性质相反D、X1与X2性质相同，X1、X2与X3性质相反
一个关系模式为Y(X1,X2,X3,X4)，假定该关系存在函数依赖：(X1,X2)→X3，X2→X4，则该关系的码为______。A．X1B．X2C．(X1，X2)D．(X1,X2,X3,X4)
设X～N(μ，σ2)，均值μ已知，而方差σ2未知，X1，X2，X3为总体X的样本，下列各式是统计量的有( )。A．X1+3X2+σ2B．X1+2μC．max(X1，X2，X3)D．(X2-μ)2/σE．
设总体X的概率密度为其中θ∈(0,+∞)为未知参数，X1，X2，X3为来自总体X的简单随机样本，令T=max(X1，X2，X3). (Ⅰ)求T的概率密度； (Ⅱ)确定a，使得aT为θ的无偏估计.
问答题设f（x）在[a，b]上连续，在（a，b）内可微，若a≥0，证明在（a，b）内存在三个数x1、x2、x3，使f′（x1）＝（b＋a）f′（x2）/（2x2）＝（b2＋ab＋a2）f′（x3）/（3x32）。
填空题设随进变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2～N（0，22），X3服从参数为λ=3的泊松分布，记随机变量Y=X1-2X2+3X3，则D（Y）=____.
填空题设数据x1，x2，x3的绝对误差为0.002，那么x1-x2-x3的绝对误差约为（）。