函数(x)=x3-6x2+9x在区间[-3,3]上的最大值为___.
函数(x)=x3-6x2+9x在区间[-3,3]上的最大值为___.
参考解析
解析:【答案】4 【考情点拨】本题主要考查的知识点为函数的最值.
【应试指导】此题是高次函数的最值问题,可用导数来求函数在区间[-3,3]上的最值.
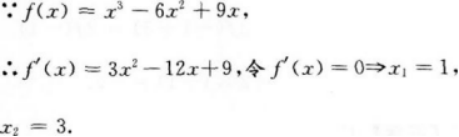
列出表格

由上表可知函数在[-3,3]上,在x=1点处有最大值4.
【应试指导】此题是高次函数的最值问题,可用导数来求函数在区间[-3,3]上的最值.
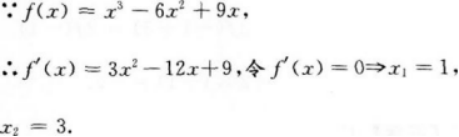
列出表格

由上表可知函数在[-3,3]上,在x=1点处有最大值4.
相关考题:
区间[a,b]上的三次样条插值函数是() A、在[a,b]上2阶可导,节点的函数值已知,子区间上为3次多项式B、在区间[a,b]上连续的函数C、在区间[a,b]上每点可微的函数D、在每个子区间上可微的多项式
设f(x)为开区间(a,b)上的可导函数,则下列命题正确的是( )。A.f(x)在(a,b)上必有最大值B.f(x)在(a,b)上必一致连续C.f(x)在(a,b)上必有D.f(x)在(a,b)上必连续
设?(x)为开区间(a,b)上的可导函数,则下列命题正确的是( )A.(x)在(a,b)上必有最大值B.(x)在(a,b)上必一致连续C.(x)在(a,b)上必有界D.(x)在(a,b)上必连续
单选题如果奇函数f(x)在区间[a,b](0<a<b)上是增函数,且最小值为2,那么f(x)在区间[-b,-a]上是( ).A增函数且最小值为-2B增函数且最大值为-2C减函数且最小值为-2D减函数且最大值为-2
单选题设P(x)是在区间[α,b]上的y=f(x)川的分段线性插值函数,以下条件中不是P(x)必须满足的条件为( )。AP(x)在[a,b]上连续BP(Xk)=YkCP(x)在[α,b]上可导DP(x)在各子区间上是线性函数
判断题开区间上的单调函数没有最大值和最小值。A对B错