设函数f(u，ν)具有2阶连续偏导数，.

设函数f(u，ν)具有2阶连续偏导数，.

参考解析

解析：【解】利用复合函数求导公式

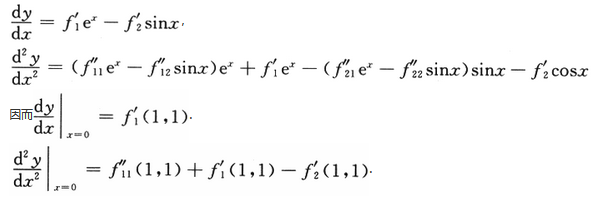
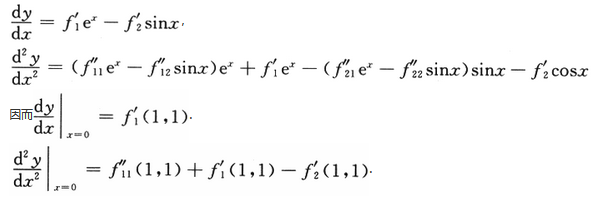
相关考题：

设函数f(x）=e5x，则f(x)的n阶导数f(n)(x)=____．
查看答案
A.只能确定一个具有连续偏导数的隐函数z=z（x，y）B.可确定两个具有连续偏导数的隐函数y=y（x，y）和z=z（x，y）C.可确定两个具有连续偏导数的隐函数x=x（x，y）和z=z（x，y）D.可确定两个具有连续偏导数的隐函数x=x（y，z）和y=y（x，z）
查看答案
设z=f(u,v)具有一阶连续偏导数，其中u=xy,v=x2+y2，A.xfu'+yfv' B. xfu'+2yfv'C.yfu'+2xfv' D.2xfu'+2yfv'
查看答案
设f（x）在区间[－a，a]（a＞0）上具有二阶连续导数，f（0）=0。f（x）的带拉格朗日余项的一阶麦克劳林公式为（　　）。
查看答案
设 , 其中f具有二阶连续偏导数, 求
查看答案
设 ,其中 具有二阶连续偏导数 具有二阶连续导数,求
查看答案
设函数在内具有二阶导数，且满足等式.
查看答案
设函数f(μ，ν)具有二阶连续偏导数，z=f(x，xy)，则=________.
查看答案
(Ⅰ)设函数u(x)，ν(x)可导，利用导数定义证明［u(x)ν(x)］’=u’(x)ν(x)+u(x)ν’(x)；　　(Ⅱ)设函数u1(x)，u2(x)，…，un(x)可导，f(x)=u1(x)u2(x)…un(x)，写出f(x)的求导公式.
查看答案
设函数z=f(xy，yg(x))，其中函数f具有二阶连续偏导数，函数g(x)可导且在x=1处取得极值g(1)=1.求
查看答案
设函数f(u)具有二阶连续导数，z=f(e^xcosy)满足　　　　若f(0)=0，f'(0)=0，求f(u)的表达式.
查看答案
已知函数f(x，y)具有二阶连续偏导数，且，其中D={(x，y)｜0≤x≤1，0≤y≤1)，计算二重积分.
查看答案
设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.
查看答案
设函数f(χ)在(-∞，+∞)内连续，其中二阶导数f”(χ)的图形如图所示，则曲线y=f(χ)的拐点的个数为( )。 A、0B、1C、2 D、3
查看答案
设函数f(χ)在(-∞，+∞)内连续，其中二阶导数f”(χ)的图形如图所示，则曲线y=f(χ)的拐点的个数为( )。 A、0B、1C、2D、3
查看答案
设f(x)具有二阶导数，y=f(x2),则的值为()。
查看答案
函数的梯度是一个（）。A、标量B、向量C、T阶偏导数D、一阶偏导数
查看答案
填空题设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝____。
查看答案
问答题设z＝f（u），而u＝u（x，y）满足u＝y＋xφ（u）。若f和φ有连续导数，u存在偏导数，且xφ′（u）≠1，证明：∂z/∂x＝φ（u）∂z/∂y。
查看答案
单选题设u＝f（x＋y，xz）有二阶连续偏导数，则∂2u/∂x∂z＝（　　）。Af2′＋xf11′＋（x＋z）f12″＋xzf22″Bxf12″＋xzf22″Cf2′＋xf12″＋xzf22″Dxzf22″
查看答案
填空题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为____。
查看答案
单选题设函数u＝u（x，y）满足∂2u/∂x2－∂2u/∂y2＝0及条件u（x，2x）＝x，ux′（x，2x）＝x2，u有二阶连续偏导数，则uxx″（x，2x）＝（　　）。A4x/3B－4x/3C3x/4D－3x/4
查看答案
单选题设偶函数f（x）具有二阶连续导数，且f″（0）≠0，则x＝0（　　）。A一定不是函数的驻点B一定是函数的极值点C一定不是函数的极值点D不能确定是否为函数的极值点
查看答案
单选题设三元函数xy－zlny＋exz＝1，根据隐函数存在定理，存在点（0，1，1）的一个邻域，在此邻域内该方程（　　）。A只能确定一个具有连续偏导数的隐函数z＝z（x，y）B可确定两个具有连续偏导数的隐函数y＝y（x，z）和z＝z（x，y）C可确定两个具有连续偏导数的隐函数x＝x（y，z）和z＝z（x，y）D可确定两个具有连续偏导数的隐函数x＝x（y，z）和y＝y（x，z）
查看答案
单选题设f有二阶偏导数，z＝f（xy），则∂2z/∂x∂y等于（　　）。Ayf″＋f′Bxy2f″Cxyf′f″Df′＋xyf″
查看答案
问答题设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。
查看答案
单选题函数的梯度是一个（）。A标量B向量CT阶偏导数D一阶偏导数
查看答案
热门标签