设随机变量X的概率密度为 对X进行独立重复的观测,直到第2个大于3的观测值出现时停止,记Y为观测次数. (Ⅰ)求Y的概率分布; (Ⅱ)求EY.
设随机变量X的概率密度为
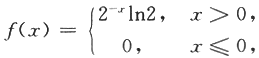
对X进行独立重复的观测,直到第2个大于3的观测值出现时停止,记Y为观测次数.
(Ⅰ)求Y的概率分布;
(Ⅱ)求EY.
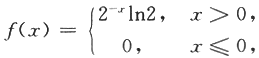
对X进行独立重复的观测,直到第2个大于3的观测值出现时停止,记Y为观测次数.
(Ⅰ)求Y的概率分布;
(Ⅱ)求EY.
参考解析
解析:【分析】令A={对X进行一次观测得到的值大于3}.

【评注】本题类似于我们在2000年出的几何分布考题.从建模到用幂级数在其收敛区间内可逐项求导求和会有不少考生感到困难,本题要比2000年的难一些.

【评注】本题类似于我们在2000年出的几何分布考题.从建模到用幂级数在其收敛区间内可逐项求导求和会有不少考生感到困难,本题要比2000年的难一些.
相关考题:
设X1,X2是任意两个相互独立的连续型随机变量,它们的概率密度分别为f1(x)与f2(x),分布函数分别为F1(x)与F2(x),则()A、f1(x)+f2(x)必为某一随机变量的概率密度B、f1(x)f2(x)必为某一随机变量的概率密度C、F1(x)+F2(x)必为某一随机变量的分布函数D、F1(x)F2(x)必为某一随机变量的分布函数
问答题设随机变量(X,Y)的概率密度为 求:(1)系数k. (2)边缘概率密度fX(x),fY(y). (3)P{X+Y1}.