旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得？A. xOy平面上的双曲线绕x轴旋转所得B. xOz平面上的双曲线绕z轴旋转所得C. xOy平面上的橢圆绕x轴旋转所得 D. xOz平面上的椭圆绕x轴旋转所得

旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得？
A. xOy平面上的双曲线绕x轴旋转所得
B. xOz平面上的双曲线绕z轴旋转所得
C. xOy平面上的橢圆绕x轴旋转所得
D. xOz平面上的椭圆绕x轴旋转所得

参考解析

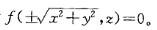
解析：提示:利用平面曲线绕坐标轴旋转生成的旋转曲面方程的特点来确定。例如在yOz平面上的曲线f(y,z) = 0,绕y轴旋转所得曲面方程为绕z轴旋转所得曲面方程为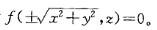

相关考题：

设曲线y=f(x)上任一点(x，y)处的切线斜率为(y/x)+x2，且该曲线经过点（1，1/2）。（1）求函数y=f(x)；（2）求由曲线y= f(x），y=O，x=1所围图形绕x轴旋转一周所得旋转体的体积V。
查看答案
将xoy面上的曲线y=x2绕y轴旋转一周所得旋转面的方程为()。
查看答案
由曲线和直线x=1，x=2，y= -1围成的图形，绕直线：y= -1旋转所得旋转体的体积为：
查看答案
将椭圆绕x轴旋转一周所生成的旋转曲面的方程是:
查看答案
椭圆x2/a2+y2/b2=1(a>b>0)绕x轴旋转得到的旋转体体积V1与绕y轴旋转得到的旋转体体积V2之间的关系为：A.V1>V2 B.V1﹤V2 C.V1=V2 D.V1=3V2
查看答案
将双曲线C：绕x轴旋转一周所生成的旋转曲面的方程是（　　）。
查看答案
将椭圆绕χ轴旋转一周所生成的旋转曲面的方程是：
查看答案
将xoz坐标面上的双曲线分别绕z轴和x轴旋转一周，则所生成的旋转曲面的方程分别为( )。
查看答案
求曲线y=，直线z=1和z轴所围成的有界平面图形的面积s，及该平面图形绕2轴旋转一周所得旋转体的体积V．
查看答案
①求曲线y=x2(x≥0)，y=1与x=0所围成的平面图形的面积S：②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy．
查看答案
求曲线y=x2与直线y=0，x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积．
查看答案
设区域D={(x，y)（0≤y≤x2，0≤x≤1)，则D绕X轴旋转一周所得旋转体的体积为（）
查看答案
①求在区间(0，π)上的曲线y=sinx与x轴所围成图形的面积S；②求①中的平面图形绕x轴旋转一周所得旋转体的体积Vx．
查看答案
求直线 绕 轴旋转一周的旋转曲面的方程，并求该曲面与平面所围立体的体积。
查看答案
设非负函数满足微分方程，当曲线过原点时，其与直线x=1及y=0围成平面区域D的面积为2，求D绕y轴旋转所得旋转体的体积
查看答案
（1）求直线y=1,曲线L以及y轴围成的平面图形绕y轴旋转一周所得到的的旋转体体积A；（2）假定曲线L绕y轴旋转一周所得到的旋转曲面为S。该旋转曲面作为容器盛满水（水的质量密度（单位体积水的重力）等于1），如果将其中的水抽完，求外力作功W.
查看答案
将平面曲线y=x2分别绕y轴和x轴旋转一周，所得旋转曲面分别记作S1和S2。(1)在空间直角坐标系中，分别写出曲面S1和S2的方程；(2)求平面y=4与曲面S1。所围成的立体的体积。
查看答案
将双曲线，绕x轴旋转一周所生成的旋转曲面的方程是（ ）。
查看答案
求由曲线y2=(x-1)3和直线x=2所围成的图形绕x轴旋转所得的旋转体的体积.?
查看答案
设D为曲线y=x2与直线y=x所围成的有界平面图形，求D绕x轴旋转一周所得旋转体的体积V.?
查看答案
(1)求曲线y=f(x)；(2)求由曲线y=f(x)，y=0，x=1所围图形绕x轴旋转一周所得旋转体体积．
查看答案
由曲线y=x2／2和直线x=1，x=2，y=-1围成的图形，绕直线y=-1旋转所得旋转体体积为：（）A、（293／60）πB、π／60C、4π2D、5π
查看答案
CAXA制造J程师软件中关于旋转面建模方法描述错误的是（）。A、旋转母线绕旋转轴线旋转可生成旋转曲面B、构造旋转曲面的旋转轴必须是直线C、构造旋转曲面的旋转母线可以是样条线D、构造旋转曲面的旋转轴必须绘制在草图中
查看答案
旋转曲面x2-y2-z2=1是下列哪个曲线绕何轴旋转所得（）？A、xOy平面上的双曲线绕x轴旋转所得B、xOz平面上的双曲线绕z轴旋转所得C、xOy平面上的椭圆绕x轴旋转所得D、xOz平面上的椭圆绕x轴旋转所得
查看答案
由曲线与直线x=1及x轴所围图形绕y轴旋转而成的旋转体的体积是（）．A、3/7πB、4/7πC、π/2D、π
查看答案
单选题方程x2/2＋y2/2－z2/3＝0表示旋转曲面，它的旋转轴是（　　）。Ax轴By轴Cz轴D直线x＝y＝z
查看答案
单选题由曲线y=x2／2和直线x=1，x=2，y=-1围成的图形，绕直线y=-1旋转所得旋转体体积为：（）A（293／60）πBπ／60C4π2D5π
查看答案
热门标签