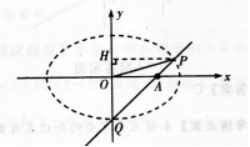
从椭圆上χ2+2y2=2的右焦点引一条倾斜45o的直线,以这条直线与椭圆的两个交点P、Q及椭圆中心。为顶点,组成△OPQ.(I)求AOPQ的周长;(Ⅱ)求AOPQ的面积.
从椭圆上χ2+2y2=2的右焦点引一条倾斜45o的直线,以这条直线与椭圆的两个交点P、Q及椭圆中心。为顶点,组成△OPQ.
(I)求AOPQ的周长;
(Ⅱ)求AOPQ的面积.
(I)求AOPQ的周长;
(Ⅱ)求AOPQ的面积.
参考解析
解析:椭圆方程变形为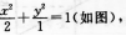

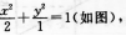


相关考题:
如图所示,已知A,B为直线L:y=mx-m+2与抛物线y=x2的两个交点。 (1)直线ι经过一个定点C,试求出点C的坐标;(2分) (2)若m=-1,已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合),且△ABP的面积为(3√13)/2,求点P的坐标。(6分)
下列关于椭圆的论述正确的个数是( )。①平面内到两个定点的距离之和等于常数的动点轨迹是椭圆②平面内到定点和定直线距离之比大于1的常数的动点轨迹是椭圆③从椭圆的一个焦点出发的射线,经椭圆反射后通过椭圆另外一个焦点④平面与圆柱面的截线是椭圆A.0B.1C.2D.3
下列关于椭圆的论述,正确的是()。A.平面内到两个定点的距离之和等于常数的动点轨迹是椭圆B.平面内到定点和定直线距离之比小于1的动点轨迹是椭圆C.从椭圆的一个焦点出发的射线,经椭圆反射后通过椭圆另一个焦点D.平面与圆柱面的截线是椭圆
下列关于椭圆的叙述,正确的是( )。A.平面内两个定点的距离之和等于常数的动点轨迹是椭圆B.平面内到定点和定直线距离之比大于1的动点轨迹是椭圆C.从椭圆的一个焦点出发的射线,经椭圆反射后通过椭圆的另一个焦点D.平面与圆柱面的截线是椭圆
已知A、B、C是椭圆上的三个点,0是坐标原点。 (1)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积; (2)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由。
下列关于椭圆的论述,正确的是()。①平面内到两个定点的距离之和等于常数的动点轨迹是椭圆②平面内到定直线和直线外的定点距离之比为大于1的常数的动点轨迹是椭圆③从椭圆的一个焦点发出的射线,经椭圆反射后通过椭圆另一个焦点④平面与圆柱面的截线是椭圆正确的个数是()。A.0B.1C.2D.3
已知中心在坐标原点0的椭圆C经过点A(2,3)且点F(2,0)为其右焦点。 (1)求椭圆C的方程; (2)是否存在平行于OA的直线l,使l与椭圆C有公共点,且直线OA与l的距离等于4,若存在,求l方程;若不存在,请证明。
在椭圆曲线定义中包含一个称为无穷远点的元素或零点,记做O,以下关于O的说法错误的是()A、O是加法的单位元。B、对椭圆曲线上的任何一点P,有P+O=P。C、假定P≠Q且Q≠0,P-P=OD、若椭圆曲线上的三个点不在一条直线上,则他们的和是O
单选题在椭圆曲线定义中包含一个称为无穷远点的元素或零点,记做O,以下关于O的说法错误的是()AO是加法的单位元。B对椭圆曲线上的任何一点P,有P+O=P。C假定P≠Q且Q≠0,P-P=OD若椭圆曲线上的三个点不在一条直线上,则他们的和是O