在下列微分方程中,以函数y=C1e^-x+C2e^4x(C1,C2为任意常数)为通解的微分方程是( )。A. y″+3y′-4y=0 B. y″-3y′-4y=0 C. y″+3y′+4y=0 D. y″+y′-4y=0
在下列微分方程中,以函数y=C1e^-x+C2e^4x(C1,C2为任意常数)为通解的微分方程是( )。
A. y″+3y′-4y=0
B. y″-3y′-4y=0
C. y″+3y′+4y=0
D. y″+y′-4y=0
B. y″-3y′-4y=0
C. y″+3y′+4y=0
D. y″+y′-4y=0
参考解析
解析:
由题意知,二阶常系数齐次线性微分方程的特征方程的两个根为-1和4,只有B项满足。
【总结】求二阶常系数齐次线性微分方程y″+py′+qy=0的通解的步骤:
①写出微分方程的特征方程r2+pr+q=0;
②求出特征方程的两个根r1,r2;
③根据r1,r2的不同情形,写出微分方程的通解:
a.当r1≠r2,

b.当r1=r2,
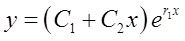
c.一对共轭复根r1,2=α±βi,y=eαx(C1cosβx+C2sinβx)。
由题意知,二阶常系数齐次线性微分方程的特征方程的两个根为-1和4,只有B项满足。
【总结】求二阶常系数齐次线性微分方程y″+py′+qy=0的通解的步骤:
①写出微分方程的特征方程r2+pr+q=0;
②求出特征方程的两个根r1,r2;
③根据r1,r2的不同情形,写出微分方程的通解:
a.当r1≠r2,

b.当r1=r2,
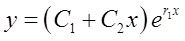
c.一对共轭复根r1,2=α±βi,y=eαx(C1cosβx+C2sinβx)。
相关考题:
在下列微分方程中,以函数y=C1e^-x+C2e^4x(C1,C2为任意常数)为通解的微分方程是( )。A. y″+3y′-4y=0 B. y″-3y′-4y=0 C. y″+3y′+4y=0 D. y″+y′-4y=0
若A、B为非零常数,C1、C2为任意常数,则微分方程y″+k2y=cosx的通解应具有形式( )。A.C1coskx+C2sinkx+Asinx+BcosxB.C1coskx+C2sinkx+AxcosxC.C1coskx+C2sinkx+AxsinxD.C1coskx+C2sinkx+Axsinx+Bxcosx
单选题设y=ex(c1sinx+c2cosx)(c1、c2为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为( )。Ay″-y′+y=0By″-2y′+2y=0Cy″-2y′=0Dy′+2y=0
单选题二阶常系数非齐次线性微分方程y″-4y′+3y=2e2x的通解为y=( )。AC1x+C2x3+2e2x(其中C1,C2为任意常数)BC1x+C2x3-2e2x(其中C1,C2为任意常数)CC1ex+C2e3x-2e2x(其中C1,C2为任意常数)DC1ex+C2e3x+2e2x(其中C1,C2为任意常数)
单选题在下列微分方程中,以y=C1ex+C2cos2x+C3sin2x(C1,C2,C3为任意常数)为通解的是( )。Ay‴+y″-4y′-4y=0By‴+y″+4y′+4y=0Cy‴-y″-4y′+4y=0Dy‴-y″+4y′-4y=0
单选题设y=ex(c1sinx+c2cosx)(c1、c2为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为( )。Ay″+2y′+2y=0By″-2y′+2y=0Cy″-2y′-2y=0Dy″+2y′+2y=0