三阶矩阵A的特征值为－2,1,3,则下列矩阵中为非奇异矩阵的是(). A.2E-AB.2E+AC.E-AD.A-3E
设A是3阶方阵，将A的第1列与第2列交换得B,再把B的第2列加到第3列得C, 则满足AQ=C的可逆矩阵Q为
设A，B为同阶可逆矩阵，则( )。A.AB=BAB.C.D.存在可逆矩阵P和Q，使PAQ=B
设A是3阶方阵，将A的第1列与第2列交换得B，再把B的第2列加到第3列得C，则满足的可逆矩阵Q为（ ?）.
设4阶矩阵A与B仅有第3行不同，且｜A｜=1，｜B｜=2，则｜A+B｜=（ ）。A.3B.6C.12D.24
设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知a是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：A. Pa B. P-1A C. PTa D.（P-1）Ta
设A是3阶矩阵，P=(a1,a2,a3)是3阶可逆矩阵，若矩阵Q=(a1,a2,a3)，则Q-1AQ=
设A，B均为4阶矩阵，且|A|=3，|B|=-2，则|-(A'B-1)2|的值为( )。
设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知α是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：(A) Pα (B) P-1α (C) PTa (D) P(-1)Ta
设A、B都是n阶可逆矩阵，则A. (-3)n A B -1B. -3 A T B TC. -3 A T B -1D. (-3)2n A B -1
设A是4×3阶矩阵且r(A)=2,B=,则r(AB)=_______.
设A1，A2分别为m阶，n阶可逆矩阵，分块矩阵.证明：A可逆，且
设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.
证明下列命题：(1) 若A，B是同阶可逆矩阵，则（AB）*=B*A*.(2) 若A可逆，则A*可逆且.(3) 若AA′=E,则.
设A=(α1，α2，α3)为3阶矩阵.若α1，α2线性无关，且α3=-α1+2α1，则线性方程组Ax=0的通解为________.
设3阶矩阵A=［α1，α2，α3］有3个不同的特征值，且a3=a1+2a2. (Ⅰ)证明r(A)=2； (Ⅱ)若β=α1，α2，α3，求方程组Ax=β的通解.
设A为四阶实对称矩阵，且A^2+A=O.若A的秩为3，则A相似于
设 都是n(n≥3）阶非零矩阵，且AB=O，则r（B）=（ ）A. 0B.1C. 2D. 3
设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知a是A的属于特征值λ的特征向量，则B的属于特征值A的特征向量是：A. PaB. P-1aC.PTaD.(P-1)Ta
设A是3阶矩阵，P=(a1,a2,a3)是3阶可逆矩阵，且P-1AP=
设A为3阶矩阵．P为3阶可逆矩阵，且A．B．C．D．
设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A、等价B、相似C、合同D、正交
设3阶矩阵，已知A的伴随矩阵的秩为1，则a=（）。A、-2B、-1C、1D、2
单选题设3阶矩阵，已知A的伴随矩阵的秩为1，则a=（）。A-2B-1C1D2
单选题设A为4阶方阵，且r（A）＝3，A*为A的伴随矩阵，则r（A*）＝（ ）。A0B1C2D3
单选题（2009）设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知α是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：（）APαBP-1αCPTαD（P-1）Tα
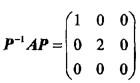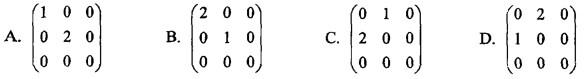
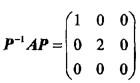，若矩阵Q=(α2，α1，α3),则Q-1AQ=( )。
。
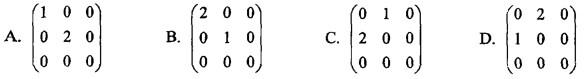
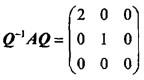
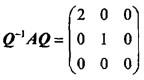