三次函数r=ax3+bx2+cx+d的导函数图象如图1， 则此三次函数的图象是( )。A． B．C．D．

三次函数r=ax3+bx2+cx+d的导函数图象如图1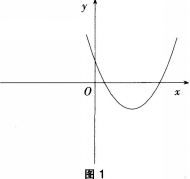， 则此三次函数的图象是( )。
A．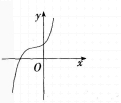
B．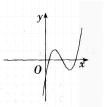
C．
D．

参考解析

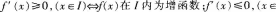
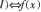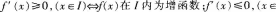
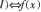解析：若f(x)在某个区间，内有导数，则在，内为减函数。结合图1中导函数的函数值从左到右依次大于0、小于0、大于0，因此原函数图象从左到右变化趋势依次是单调递增、单调递减、单调递增。因此选B。

相关考题：

若反比例函数的图象经过点A(-2,1) ,则它的表达式是 _________________ ．
查看答案
表示逻辑函数通常使用真值表、逻辑函数、卡诺图、逻辑图及工作波形图。 () 此题为判断题(对，错)。
查看答案
若函数F和函数G的卡诺图相同,则函数F'和函数G相等。() 此题为判断题(对，错)。
查看答案
在同一直角坐标系内一次作出函数y=x+1，y=2x+1，y=3x+1的图象。（1）这几个图象之间有什么差别，又有什么联系？（2）一次函数y=kx+b的一次项系数k对函数的图象有什么影响？
查看答案
已知函数 y=x²-4x+3。（1）画出函数的图象；（2）观察图象，当x取哪些值时，函数值为0？
查看答案
画出函数 y=x²-2x-3的图象，利用图象回答：（1）方程 x²-2x-3=0 的解是什么；（2）x取什么值时，函数值大于0 ；（3）x取什么值时，函数值小于0 。
查看答案
已知一次函数的图象经过点A（2，1），B（－1，－3）（1）求此一次函数的解析式；（2）求此一次函数的图象与x轴、y轴的交点坐标；（3）求此一次函数的图象与两坐标轴所围成的三角形面积。
查看答案
函数f(x)的导函数f'(x)的图像如右图所示，则在(－∞，＋∞)内f(x)的单调递增区间是（）A.(－∞，0)B.(－∞，1)C.(0，＋∞)D.(1，＋∞)
查看答案
A.常数k＜-1B.函数f(x)在定义域范围内，y随着x的增大而减小C.若点C(-1，m)，点B(2，n)，在函数f(x)的图象上，则m＜nD.函数f(x)图象对称轴的直线方程是y=x
查看答案
下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)． (1)求出图象与戈轴的交点A，B的坐标； 存在，请说明理由； ° (3)将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b(b＜1)与此图象有两个公共点时，b的取值范围．
查看答案
定义[a，b，c]为函数y=ax2+bc+c的特征数，下面给出特征数为[ 2m ，1-m，-1-m]的函数的一些结论： ①当m=-3时，函数图象的顶点坐标是{1/3,-(8/3)}； ②当m>0时，函数图象截石轴所得的线段长度大于3/2； ③当m1/4时，y随x的增大而减小； ④当m≠0时，函数图象经过同一个点。 其中正确的结论有()。A.②③④B.①②④C.③④D.②④
查看答案
用梅逊公式（或方块图简化）计算如图总的传递函数G（s）=C（s）／R（s），结果应为（　　）。
查看答案
简支梁某段长度上受有均布载荷q，则该段粱的挠度y，是沿轴线的横坐标x的( )。A 五次函数B 四次函数C 三次函数D 二次函数
查看答案
初中数学《二次函数的图象与性质》一、考题回顾题目来源:5月18日 上午 湖北省黄石市 面试考题试讲题目1.题目：二次函数的图象与性质2.内容：3.基本要求：(1)掌握五点作图法的画图方法，能根据图象理解二次函数的性质;(2)试讲十分钟;(3)要有合适的板书。答辩题目1.二次函数 的顶点坐标如何表示?2.确定二次函数的表达式需要几个条件?
查看答案
函数y(x)的导函数f(x)的图象如图所示，Xo=-1，则( )A、X。不是驻点B、x。是驻点，但不是极值点C、x。是极小值点D、 X。极大值点
查看答案
“函数图象”是高中数学中很重要的知识点，通过复习所学函数模型及其图象特征．可以使学生对函数有一个较直观的把握和较形象的理解，缓解因函数语言的抽象性引起的学生的心理不适应及不自觉的排斥情绪。 (1)关于“函数图象及其应用”给出你的教学设计目标。(10分) (2)确定教学重点、难点。(10分) (3)设置两个教学环节(给出两个以上例题或练习题)并说明设计意图。(10分)
查看答案
函数y=-χ·cos的部分图象是( )。
查看答案
光滑函数f(χ)的图象如图所示，下列关系式正确的是( )。
查看答案
三次函数y=aχ3+bχ2+cχ+d的导函数图象如图l． 则此三次函数的图象是( )。
查看答案
关于二次函数y=2-(x+1)2的图象,下列说法正确的是( )。A.图象开口向上B.图象的对称轴为直线x=1C.图象有最低点D.图象的顶点坐标(-1，2)
查看答案
若函数f(x)=(k-1)ax- ax (a＞0且α≠1)在R上既是奇函数，又是减函数，则g(x)=loga (x+k)的图象是( )。
查看答案
一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k0；③当xA.0B.1C.2D.3
查看答案
若函数f(x)的图象上点P(1，m)处的切线方程为3x-y+b=0，则m的值为__________。
查看答案
已知函数f(x)=x2+4lnx． (1)求函数f(x)在[1，e]上的最大值和最小值； (2)证明：当x∈[1，+∞)时，函数八戈)的图象在g(x)=2x3的图象的下方。
查看答案
已知函数 (x)=sin(ωx+φ)(ω>0)的图象如下图所示，则ω=（　　）。
查看答案
硬化曲线的函数表达式通常采用（）。A、幂函数B、指数函数C、二次函数D、三次函数
查看答案
单选题硬化曲线的函数表达式通常采用（）。A幂函数B指数函数C二次函数D三次函数
查看答案
热门标签