一元二次方程专题训练测试题
如果2是一元二次方程x2+bx+2=0的一个根,那么常数b的值为________________.
-3
曲线y=x3—2x在点(1,-1)处的切线方程为 .
y=x-2【考情点拨】本题主要考查的知识点为切线方程.【应试指导】
解方程。
X-0.25=1/4 X/4=30%
4+0.7X=102 2/3X+1/2X=42
X-0.25=1/4 X/4=30%
X=1/4+0.25 X=30%×4
X=0.5 X=1.2
4+0.7X=102 2/3X+1/2X=42
0.7X=102-4 7/6X=42
X=140 X=36
解下列方程:
(1)4x-2=3-x ;
(2)-7x+2=2x-4 ;
(3)-x=-2x/5+1
(4)2x-1/3=-x/3+2
(1)x=1
(2)x=2/3
(3)x=-5/3
(4)x=1
打开考生文件夹下的DB数据库,完成如下简单应用: 1.编写一个名为FOUR.PRG的程序,根据表TABA中所有记录的a,b,c三个字段的值,计算各记录的一元二次方程的两个根x1和x2,并将两个根x1和x2写到对应的字段x1和x2中,如果无实数解,在note字段中写入“无实数解”。提示:平方根函数为SQRT;程序编写完成后,运行该程序计算一元二次方程的两个根。注意:一元二次方程公式如下: 2.打开名为testA的表单,其中有两个命令按钮,界面要求如下: (1)设置两个按钮的高度均为30,宽度均为80,“退出”按钮与“查询”按钮顶边对齐。 (2)“查询”按钮的功能是在该按钮的Click事件中使用SQL的SELECT命令从表TABA中查询“无实数解”的记录并存储到表TABD中。 (3)“退出”按钮的功能是关闭并释放表单。 请按要求完成表单的设计,表单设计完成后,运行该表单,并单击“查询”按钮进行查询。
2.打开名为testA的表单,其中有两个命令按钮,界面要求如下: (1)设置两个按钮的高度均为30,宽度均为80,“退出”按钮与“查询”按钮顶边对齐。 (2)“查询”按钮的功能是在该按钮的Click事件中使用SQL的SELECT命令从表TABA中查询“无实数解”的记录并存储到表TABD中。 (3)“退出”按钮的功能是关闭并释放表单。 请按要求完成表单的设计,表单设计完成后,运行该表单,并单击“查询”按钮进行查询。
(1)【操作步骤】
新建程序four,并输入以下命令:
*******”four”程序文件中的代码*******CLOSALL
USETABASCAN
IFA<>0ANDB*B一4*A*C>=0
REPLx1WITH(-B+SQRT(B*B一4*A*C))/(2*A),x2WITH(-B-SQRT(B*B一4*A*C))/(2*A)
ELSE
REPLNOTEWITH”无实数解”ENDIF
ENDSCAN****************************
最后保存运行程序。
(2)【操作步骤】
步骤1:打开表单“testA”。
步骤2:按Shift的同时选中“查询”和“退出”两个按钮,然后在属性窗口设定它们的Height属性为30,Width属性为80,在系统菜单中选择“格式”→“对齐”→“顶边对齐”。
步骤3:在“查询”按钮的Click事件中输入下列代码。
*******”three”程序文件中的代码*******
SELECT*;FROMTABA;WHERETABA.note=”无实数解”;
INTOTABLETABD.dbf
****************************
步骤4:在“退出”命令按钮的Click事件中输入“This.
Form.Release”。保存并运行表单。
摘要:一元二次方程专题训练一、选择题1、下列方程中,一元二次方程是(2(A)x)1(B)ax2bx(C)x1x21(D)3x22xy5y202x2、方程2x3x11的解的情况是()(A)有两个不相等的实数根(B)没有实数根(C)有两个相等的实数根(D)有一个实数根3、下列二次三项式在实数范围内不能分解因式的是()(A)6x2x15(B)3y27y3(C)x22xy4y2(D)2x24xy5y24、若方程3x25x70的两根为x1、x2,下列表示根与系数关系的等式中,正确的是(x27(A)x1x25,x1�53(C)x1x2,x1�x2735353(D)x1x2,x1�x25、已知x1、x2是方程x22x1的两个根,则(A)11(B)2(C)226、方程ax2bxc073(B)x1x2,x1�x27311的值为(x1x2)(D)-2b0a0、、c0的两个根的符号为()(A)同号(B)异号(C)两根都为正(D)不能确定7、已知方程x2m1x3m0的两个根是互为相反数,则m的值是()2(A)m12(B)m1(C)m1(D)m08、如果一元二次方程x2m1xm0的两个根是互为相反数,那么()(A)m=0(B)m=-1(C)m=1(D)以上结论都不对9、方程x20的实数根的个数是()(A)1个(B)2个(C)0个(D)以上答案都不对10、若方程x2mxn0中有一个根为零,另一个根非零,则m,n的值为()(A)m0
一元二次方程x2+x-2=0 的两根之积是( )
A.-1
B.-2
C.1
D.2
【应试指导】由x2+y2=2x,两边对x求导得2x+
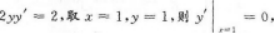
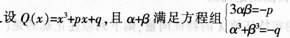 (1)证明α+β是Q(χ)=0的根;(3分)
(1)证明α+β是Q(χ)=0的根;(3分)
(2)写出以α3和β3为根的一元二次方程。(4分)

【教师甲】
设置问题:请同学们根据下列问题,只列出含未知数的方程:
(1)一个正方形的面积为2,求正方形的边长x。

预设:学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排序,右侧为零的形式,然后引导学生完成下面两件事:对比“一元一次方程”的定义,为这类方程定义一个名称——一元二次方程。再请学生自行写出几个不同的一元二次方程,并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问:什么是“一元一次方程”?请你根据“一元一次方程”的定义,给出“一元二次方程”的定义,并举出几个“一元二次方程”的例子。在学生举例的基础上,提炼出“一元二次方程”的一般表达式。
请完成下列任务:
(1)请分析两位老师引入“一元二次方程”概念设计方案的各自的特点。(15分)
(2)在教学中,当引入一个新的数学概念之后,往往通过例题、习题加深对概念的理解。请针对“一元二次方程”概念,设计不同难度的两道例题和两道练习题,加深学生对“一元二次方程”概念的理解。(15分)
(1)教学活动是师生积极参与、交往互动、共同发展的过程。有效的教学活动是学生学与教师教的统一,学生是学习的主体,教师是学习的组织者、引导者和合作者。数学教学活动应激发学生的学习兴趣,调动学生积极性,引发学生思考,鼓励学生的创造性思维。在教学的过程中教师应培养学生良好的数学学习习惯,使学生掌握恰当的数学学习方法。也注重以学生的认知发展水平和已有经验为基础,面向全体学生,采取启发式和因材施教的教学。学生在生动活泼的、主动的教学课堂中,更容易吸收知识,但也应注重多种学习方式相结合,除接受学习外,动手实践、主动探索与合作交流同样是学习数学的重要方式。
教师甲的教学方案,相对于乙教师来说,更加非常符合素质教育的要求。
(2)针对“一元二次方程”概念,设计不同难度的两道例题和两道练习题,题目的难度应适当,目的是加深学生对“一元二次方程”概念的理解。
【教师甲】
设置问题:请同学们根据下列问题,只列出含未知数x的方程:
(1)一个正方形的面积为2,求正方形的边长x。
(2)长度为1的线段AB有一点C,且满足AC/AB=BC/AC,求线段AC的长x。
预设:学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排列,右侧为零的形式,然后引导学生完成下面两件事:对比”一元一次方程“的定义,为这类议程定义一个名称——一元二次方程。再请学生自行写出几个不同的一元二次议程,并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问:什么是“一元一次方程”?请你根据“一元一次方程”的定义,给出“一元二次方程”的定义,并举出几个“一元二次方程”的例子。在学生举例的基础上,提炼出“一元二次方程”的一般表达式。
请完成下列任务:
(1)请分析两位老师引入“一元二次方程”概念设计方案的各自的特点。
(2)在教学中,当引入一个新的数学概念之后,往往通过例题、习题加深对概念的理解。请针对“一元二次方程”概念,设计不同难度的两道例题和两道习题,以加深学生对“一元二次方程”概念的理解。
教师甲的做法非常符合素质教育的要求的,在教学中体现教师的组织者、引导者作用,学生的主体地位,在学生已有知识的基础上预设了正面的教学环境,先让学生利用已有的知识,列出相应的方程,再逐步引进新的教学内容,对比一元一次和一元二次方程的区别,进而引导学生总结出一元二次方程的概念,体现了螺旋上升课堂内容安排和预设与生成的要求,同时也充分地调动了学生学习的积极性和主动性,是非常好的课堂设计。
教师乙的做法相对教师甲来说,是有所欠缺的,没有给学生预设情境,直接让学生去生成一元二次方程的概念,加大了学生接受新知识的难度,同时还不利于学生对新知识的透彻理解,虽然体现了学生的主体地位,但是老师的引导作用没有充分发挥。
(2)概念的引入例子
引例1:
剪一块面积是150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应如何剪?

设长方形宽为xcm,则有x(x+5)=150整理得x2+5x-150=0。
引例2:
学校图书馆去年年底有图书5万册,预计到明年年底有7.2万册,求这两年的平均增长率。
设这两年的平均增长率为x,则今年年底的图书数是5(1+x)万册,明年年底的图书数是5(1+x)(1+x)=5(1+x)2万册。
可列得方程5(1+x)2=7.2
概念的巩固例子
例子1:
下列方程都是整式方程吗?其中哪些是一元一次方程,哪些是一元二次方程?
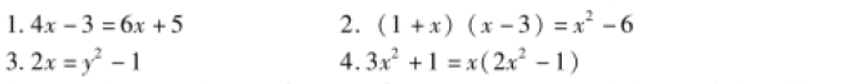
例子2:关于x的方程mx2-3x=x2-mx+2是一元二次方程的条件是什么?
相关考题:
- 几何公差带形状是距离为公差值t的两平行平面内区域的有()
- 单位通知存款不论实际存期多长,均按存款人提前通知银行取款的期限划分为1天和7天两种。
- 中长期贷款展期不得超过原贷款期限的一半,最长不得超过5年.
- 马汉认为海军是什么性质的军种?
- 本行为付款行,对方行为收款行的网内往来汇划业务是发出贷方报单业务。
- 能源地缘政治的风险它会影响到哪些方面?
- ( 难度:中等)Hive适用于以下哪些应用场景A.统计上个月在网用户数B.计算近十年人均话费变化趋势C.实时计算用户套餐剩余量D.疫情期计算用户行程数据
- ( 难度:中等)在sql的查询语句中,不能用于分组查询的语句是A.group byB.order byC.havingD.limit
- ( )是我们后天慢慢习得的一种社会规范和道德,亦即被内化的道德。A.自我B.超我C.本我D.自性
- “转移”这种自我防御机制的含义是( )A.成年人遇到难过的事或遭受打击时心理和生理退回到较早期的状态B.将指向某一对象的情绪或幻想转移到另一个对象或替代的象征物上C.把感到危险或痛苦的想法排除在意识之外使之不被察觉D.拒绝承认不愉快的现实