(必考题)小学数学五年级上册第四单元可能性检测(答案解析)
口袋里有3个红球和2个白球,球除颜色外完全相同,从中任意摸出1个球。那么,摸出红球的可能性是_____,摸出白球的可能性是_____。要使它们的可能性相同,可以怎么做?
3/5;2/5;拿走一个红球
流水线上生产的小木球涂色的顺序是:先5个红,再4个黄,再3个绿,再2个黑,再1个白,然后再依次如此涂色,那么第2006个小球涂( )颜色。
A.红
B.白
C.黑
D.绿
【解析】木球颜色变化按照15为一组循环,因此用2006除以(5+4+3+2+1),观察余数的位置就可以做出判断。答案选D。
某工厂流水线上生产彩色小木球的次序是:先 5 个红,再 4 个黄,再 3 个绿,再 2 个
黑,再 1 个白,然后依次 5 红、4 黄、3 绿、2 黑、1 白……继续下去,那么,第 2004个小球
的颜色是什么色?( )
A.红
B.黄
C.绿
D.黑
(3)一个口袋内装有除颜色外其他都相同的6个白球和4个红球,从中任意摸出2个,求:A、2个都是白球的概率;B、2个都是红球的概率;C、一个白球,一个红球的概率。
箱子里有红、白两种玻璃球,红球是白球的3倍少2个。每次从箱子里取出7个白球、13个红球,经过若干次后,箱子里剩下6个白球,72个红球,那么,原来箱予里红球比白球多多少个?( )
A.102
B.104
C.106
D.108
D[解析]假设箱子里原来有白球x个,那么红球为(3x-2)个,依题意有(x-6)÷7=(3x-2-72)÷13,解得x=55,所以原来红球比白球多3×55-2-55=108(个)。故选D。
必考题)小学数学五年级上册第四单元可能性检测(答案解析)一、选择题1在下列情况中,()箱里的红球更容易摸出A.8白,1红,3黑B.5蓝,5白,2红C.4红,4白,4黑2五一班同学玩摸球游戏(每人摸一次,然后放回再摇匀)。52人中,12人摸到了白球,40人拨到了红球。那么箱子中最有可能装有()。A.5个红球,5个白球B.2个白球,8个红球C.8个白球,2个红球D.12个白球,4个红球3小军给同学打电话,忘记了号码中的最后一个数字,只记得这个数字是单数,他随意拨打,最多可能拨打()次可以拨打成功A.5B.4C.24用“剪刀、石头、布”的方法决定谁先走,对方先出什么的可能性大?()A.出剪刀B.出布C.出石头D.三种可能性一样大5将分别写有3,7,6三个数字的卡片反扣在桌面上,任意抽两张,和是奇数的可能性()和是偶数的可能性。A.大于B.小于C.等于D.无法确定6口袋里有1个红球、2个白球、3个黑球和4个黄球。任意摸一个,摸到()球的可能性最大。A.红B.白C.黑D.黄7盒子里装有黑、白两种颜色的球,安安从中摸出一个球后再放回去摇匀,重复20次并记录下球的颜色,情况如下表。如果安安再摸一次,下面哪句话的描述是正确的?A.一定摸到黑球B.一定摸到白球C.摸到黑球的可能性比较大D.摸到白球的可能性比较大8如图,多次转动转盘,指针经常停在()处。A.唱歌B.讲故事C.无法确定9今天是元旦,西安明天()会下雪。A.一定B.可能C.不可能10下面是从纸袋中摸30次跳棋的结果(摸出一个棋子后再放回去摇匀),则纸袋中()。记录次数白棋正黄旗正正正正帀24A.白棋数量多B.黄棋数量多C.白棋和黄棋数量一样多11王老师要给小强家打电话,可是一时忘记了其中一个数,只记得是2775*45,他随意拨打,恰好拨通的可能性是()A.12天气预报已经成为人们日常生活必不可少的每日信息,这里应用了统计与可能性的知识请你想一想:某日天气预报为:多云转小雨,27C12C,降水概率80%,这天一定下雨吗?定不一定某日天气预报为:晴转多云,28C14C,降水概率30%,这天一定不下雨吗?A.一定B.不一定二、填空题13抽签游戏:讲故事5张,唱歌3张,跳舞1张,我最有可能表演。14瓶子里装着8个牛奶糖,3个水果糖,哲哲取出1个,是的可能性大,是的可能性小。A.牛奶糖B.水果糖C.无法确定15盒子里有1个白球,2个红球,3个黄球,任意摸出1个,有种结果,摸到球的可能性最大,摸到球的可能性最小。16如图:转盘指针停在的可能性最大,停在的可能性最小。|不丿17口袋里有8个球,球上分别写着1、2、3、4、5、6、7、8。任意摸出一个球,共有种可能。游戏中,“摸出比4大的数”算小明赢,“摸出比4小的数”算小红赢,赢的可能性大。18一个盒子里有7个白球和2个红球。任意摸出一个,可能出现种情况,摸出的可能性大。19白天过去就是黑夜,这是发生的。(填“一定”或“可能”)20某商场搞促销,凡是购物满500元,即有一次机会转动转盘(如图)。转动转盘后,指针指向几,就获得几等奖。获得等奖的可能性最大,获得等奖的可能三、解答题21把6张卡片放入纸袋,随意摸一张,要使摸出数字“1”的可能性最大,数字“5”的可能1)不可能抽出唱歌、跳舞、讲故事以外的内容。2)抽到唱歌的可能性最大。3)抽到讲故事的可能性最小。23我能连得对面有5个愿望,请你为每个愿望选个盒子,使这些愿望最有希望实现(1)想取一个黄球口袋里有一些形状和大小相同、颜色不同的球,怎样设计能使摸到红球的可能性是/在一个正方体的6个面上分别标上数字,使得“2朝上的可能性为,可以怎样办?26把10张卡片放入盒子,随意摸一张,要使摸出数字“2”的可能性最大,数字“4”的可能性最小,卡片上可以是什么数字?请你填一填。参考答案】*试卷处理标记,请不要删除一、选择题1C解析:C/【解析】【解答】选项A,“(8+1+3)=-;选项B,2一(5+5+2)=:;选项C,4=(4+4+4)=;/因为所以4红,4白,4黑这个箱子里的红球更容易摸出。故答案为:C。【分析】此题主要考查了可能性的知识,分别用除法求出各箱中红球摸到的可能性,然后比较大小即可解答。2B解析:B【解析】【解答】40=12=4,箱子里最有可能装有2个白球,8个红球。故答案为:B。【分析】此题主要考查了可能性的应用,根据摸球的结果可知,摸到红球的可能性大致是白球的4倍,则箱子里红球的个数可能是白球的4倍,据此解答。3A解析:A【解析】【解答】102=5(次)故答案为:A。【分析】09共10个数字,单数有5个,最多可能拨打5次可以拨打成功4D解析:D【解析】【解答】用“剪刀、石头、布”的方法决定谁先走,对方先出三种可能性一样大。故答案为:D。【分析】用“剪刀、石头、布”的方法决定谁先走,这个游戏是公平的,每个人赢的可能性大小相等,据此解答。5A解析:A【解析】【解答】3+7=10,3+6=9,7+6=13,和是奇数的情况有2两种,和是偶数的情况有1种,任意抽两张,和是奇数的可能性大于和是偶数的可能性。故答案为:A。【分析】根据题意可知,先求出三个数字中每两个数字的和,然后判断和是奇数还是偶数,然后判断可能性的大小,据此解答。6D解析:D【解析】【解答】口袋里有1个红球、2个白球、3个黑球和4个黄球。任意摸一个,摸到黄球的可能性最大。故答案为:D。【分析】哪种的数量最多,摸到哪种球的可能性就最大。7C解析:C【解析】【解答】如果安安再摸一次,摸到黑球的可能性比较大。故答案为:C。【分析】观察记录表可知,重复20次,摸到黑球18次,摸到白球2次,说明盒子里装的黑球较多,盒子里什么颜色的球多,摸到什么颜色的球次数就多。数学上叫做摸到什么颜色的可能性就大。8A解析:A【解析】【解答】多次转
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。


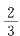 ,假设取到白色1号球,则第二次必须 取到黑色1号球,其概率为
,假设取到白色1号球,则第二次必须 取到黑色1号球,其概率为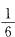 。因此前两次恰好摸到同编号的异色球的概率为
。因此前两次恰好摸到同编号的异色球的概率为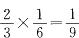 。。
。。

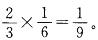
(1)一次性抽取4个球;(2)逐个抽取,取后无放回;(3)逐个抽取,取后放回.
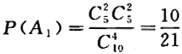
(2)设A2={逐个抽取4个球,取后不放回,其中2个红球2个白球},则
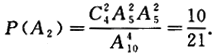
(3)设A3={逐个抽取4个球,取后放回,其中2个红球2个白球},则
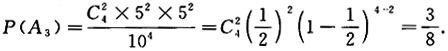
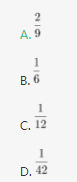

相关考题:
- 单选题( )是由《保险法》以列举方式直接规定的法定条款。A保证条款B特约条款C基本条款D附加条款
- 艺术是通过()具体的反映生活,表现作者思想感情的一种社会意识形态。
- 挂失止付按挂失的形式分为()A、口头挂失B、书面挂失C、凭证挂失D、密码挂失E、永久挂失
- 案件线索的可疑现象中内部账户突然出现大额往来及不明款项长时间或多次挂账属于()。A、内外账务不符B、柜面可疑业务C、客户投诉或信访举报反映的问题D、员工异常行为
- 针对客户无正当理由要求提供上门服务、欺诈、无理取闹、寻衅滋事、炒作是非等情形,营业机构要及时向上级行业务管理部门报告。
- 贷款集中度控制是属于商业银行()。A、流动性监管B、经营性监管C、准入监管D、市场退出监管
- 多选题根据近因原则,下列处理正确的是( )。A连续发生的原因都是被保风险,保险人赔偿全部损失B连续发生的原因中含有除外风险,前因是被保风险,后因是除外风险,后因是前因的必然结果,则保险人对损失负全部责任C连续发生的原因中含有除外风险,后因是被保风险,前因是除外风险,后因是前因的必然结果,则保险人对损失负全部责任D间断发生的多项原因造成的损失,并且都是除外风险,保险人不承担赔偿责任
- 多选题规定投保人在保险事故发生后履行通知义务的目的是( )。A使保险人得以迅速调查事实真相,防止因证据灭失而影响责任的确定B便于保险人及时采取措施,协助被保险人抢救被保险财产,处理保险事故C使保险人有准备赔偿或给付保险金的必要时间D防止投保人欺诈
- 在日常经营活动中要多进多发优秀出版物,坚决不进不销宣扬()以及法律、法规禁止的出版物,不进不销盗版、盗印的出版物和非法出版物。
- 多选题保险公司的促销策略包括( )。A广告促销B公共关系促销C人员促销D上门推销