一个盒子中5个红球,5个白球,现按照如下方式,求取到2个红球和2个白球的概率. (1)一次性抽取4个球;(2)逐个抽取,取后无放回;(3)逐个抽取,取后放回.
一个盒子中5个红球,5个白球,现按照如下方式,求取到2个红球和2个白球的概率.
(1)一次性抽取4个球;(2)逐个抽取,取后无放回;(3)逐个抽取,取后放回.
(1)一次性抽取4个球;(2)逐个抽取,取后无放回;(3)逐个抽取,取后放回.
参考解析
解析:【解】(1)设A1={一次性抽取4个球,其中2个红球2个白球),则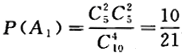
(2)设A2={逐个抽取4个球,取后不放回,其中2个红球2个白球},则
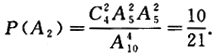
(3)设A3={逐个抽取4个球,取后放回,其中2个红球2个白球},则
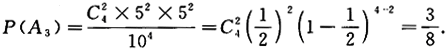
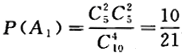
(2)设A2={逐个抽取4个球,取后不放回,其中2个红球2个白球},则
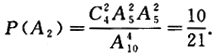
(3)设A3={逐个抽取4个球,取后放回,其中2个红球2个白球},则
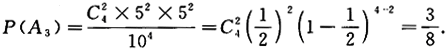
相关考题:
为了庆祝新年,“必胜客”举行赠送比萨抽奖活动。活动规则如下:在一个抽奖盒子里,共装有2 个红球、3 个 白球和4 个蓝球。每抽到一个白球就赠送比萨一个。那么,抽到白球的概率大概是多少?A.9.9% B.13.5% C.33.3% D.45%
现有三个箱子,第一个箱子有4个红球,3个白球;第二个箱子有3个红球,3个白球;第三个箱子有3个红球,5个白球;先取一只箱子,再从中取一只球,(1)求取到白球的概率;(2)若取到红球,求红球是从第二个箱子中取出的概率.
有三个盒子,第一个盒子有4个红球1个黑球,第二个盒子有3个红球2个黑球,第三个盒子有2个红球3个黑球,如果任取一个盒子,从中任取3个球,以X表示红球个数. (1)写出X的分布律;(2)求所取到的红球数不少于2个的概率.
袋中有1个红球、2个黑球与3个白球,现有放回地从袋中取两次,每次取一个球.以X,Y,Z分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求P{X=1|Z=0};(Ⅱ)求二维随机变量(X,Y)的概率分布.
三个相同的盒子里各有2个球,其中一个盒子里放了2个红球,一个盒子里放了2个蓝球,一个盒子里放了红球和蓝球各1个。随机选择一个盒子后从中随机摸出一球是红球,则这个盒子里另一个球是红球的概率为( )。A.1/2B.3/4C.2/3D.4/5
甲盒内有红球4只,黑球2只,白球2只;乙盒内有红球5只,黑球3只;丙盒内有黑球2只,白球2只,从这三只盒子的任意一只中任取出一只球,它是红球的概率是( )A.0.5625B.0.5C.0.45D.O.375E.0.225
一个口袋中有7个红球3个白球,从袋中任取一球,看过颜色后是白球则放回袋中,直至取到红球,然后再取一球,假设每次取球时各个球被取到的可能性相同,求第一、第二次都取到红球的概率( )。A.7/10B.7/15C.7/20D.7/30
为了庆祝新年,“必胜客”举行赠送比萨抽奖活动。活动规则如下:在一个抽奖盒子里,共装有2个红球、3个白球和4个蓝球。每抽到一个白球就赠送比萨一个。那么,抽到白球的概率大概是多少( )A、9.9%B、13.5%C、33.3%D、45%
单选题一只盒子中有红球m个,白球10个,黑球n个,每个球除颜色外其他都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( ).Am=4,n=6Bm=5,n=5Cm+n=5Dm+n=10
单选题为了庆祝新年,“必胜客”举行赠送比萨抽奖活动。活动规则如下:在一个抽奖盒子里,共装有2个红球、3个白球和4个蓝球。每抽到一个白球就赠送比萨一个。那么,抽到白球的概率大概是多少?()A9.9%B13.5%C33.3%D45%
问答题8.袋中有7个球,其中红球5个白球2个,从袋中取球两次,每次随机地取一个球,取后不放回,求: (1)第一次取到白球、第二次取到红球的概率; (2)两次取得一红球一白球的概率.