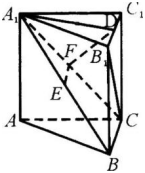
如图，在直三棱柱ABC—A1B1C1中，E，F分别是A1B，A1C的中点，点D在B1C，上，A1D⊥B1C，求证：(8分)(1)EF∥平面ABC；(2)平面A1FD上平面BB1C1C．

如图，在直三棱柱ABC—A1B1C1中，E，F分别是A1B，A1C的中点，点D在B1C，上，A1D⊥B1C，求证：(8分)
(1)EF∥平面ABC；
(2)平面A1FD上平面BB1C1C．

参考解析

解析：证明：(1)由E，F分别是A1B1A1C的中点知，EF∥BC，

相关考题：

工作表sheet1的A1单元格的完整地址表示为()。 A、Sheet1:A1B、sheet1!A1C、sheet1→A1D、sheet1+A1
查看答案
在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线,求证:M与N分别是AC和CD的中点。
查看答案
在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。A．2.5B．5C．10D．15
查看答案
如图：已知圆0，点P在圆外，D，E在圆上，PE交圆于C，PD与圆相切，G为CE上一点且满足PG=PD,连接DG并延长交圆于A，作弦AB⊥EP，垂足为F。 (1)求证：AB为圆的直径； (2)若AC=BD，AB=5，求弦DE的长。
查看答案
如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。 A.12B.14C.15D.16
查看答案
如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.(1)求证：AB=BC； (2)当BE⊥AD于E时，试证明：BE=AE+CD.
查看答案
已知两个共用一个顶点的等腰Rt△ABC，等腰Rt△CEF，∠ABC=∠CEF= 90o，连接AF，M是AF的中点，连接MB，ME。 (1)如图1，当CB与CE在同一直线上时，若CB=a，CE=2a，求BM，ME的长； (2)如图2,当∠BCE=45o时，求证：BM=ME。
查看答案
如图，三棱柱ABC-A1B1C1，M，N分别为AB，B1C1的中点， (1)求证MN∥平面AA1C1C； (2)若C1C=CB1，CA=CB，平面CC1B1B⊥平面ABC，求证：AB⊥平面CMN。
查看答案
正三棱柱ABC—A/B/C/，底面边长为a，侧棱长为h．(I)求点A到△A/BC所在平面的距离d；(Ⅱ)在满足d=1的上述正三棱柱中，求侧面积的最小值．
查看答案
如图所示，有一束平行于等边三棱镜截面ABC的单色光从空气射向E点，并偏折到F点。已知入射方向与边AB的夹角为θ=30。，E、F分别为边AB、BC的中点，则（　　）。
查看答案
如图所示，在长方形ABC.D中，AD=2AB，E为BC.的中点，F为EC.上任意一点（与E点、C.点不重合），从图形6个点中随机选取3个，能构成直角三角形的概率为：A.1/2B.9/20C.7/20D.2/5
查看答案
如图3，△ABC向右平移后得到△DEF，且点B、C、E、F在同一直线上，已知BF=8，CE=2，则平移的距离是__________。
查看答案
在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则( )。A、2B、4C、5D、10
查看答案
如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。
查看答案
(10分)如图，四棱锥P-ABCD的底面为正方形，侧棱PD⊥底面ABCD，点E为棱PA的中点，PD=AD=1。 (1)求证：PC∥平面BDE： (2)求三棱锥B-PDE的体积。
查看答案
(10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。 求证：(1)AE⊥BC；(3分) (2)求异面直线AE与DC所成角的余弦值。(7分)
查看答案
在STM—N信号中，帧定位的字节是（）。A、A1B、B1C、A2D、B2
查看答案
在SDH网络中用于传送同步精度等级的是哪一个字节？（）A、A1B、B1C、D1D、C2E、S1F、K1
查看答案
香料烟中一级的代号为（）A、A1B、B1C、A2D、K1
查看答案
以下（）字节是VC4的跟踪字节。A、A1B、B1C、J0D、J1
查看答案
香料烟B1的颜色为（）A、A1B、B1C、A2D、K1
查看答案
以下字节是复用段保护时用来传递复用段节点信息的是（）。A、A1B、B1C、C1D、K1E、K2
查看答案
下字节是用来检测信号帧头的是（）。A、A1B、B1C、C1D、K1E、A2
查看答案
Excel工作表第一个单元格对应的地址是（）。A、A1B、B1C、A2D、B2
查看答案
核心客户分布象限包括（）。A、A1B、B1C、B2
查看答案
在可信任计算机标准评估准则中，安全等级最低的是（）A、A1B、B1C、C1D、D1
查看答案
无卸荷槽的（）等级修车轴可装用在提速货车上。A、A1B、B1C、C1D、D1
查看答案
热门标签