如图3,△ABC向右平移后得到△DEF,且点B、C、E、F在同一直线上,已知BF=8,CE=2,则平移的距离是__________。
如图3,△ABC向右平移后得到△DEF,且点B、C、E、F在同一直线上,已知BF=8,CE=2,则平移的距离是__________。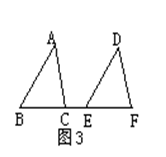

参考解析
解析:5
相关考题:
任画一个Rt△ABC,其中∠B=90°,分别作出△ABC按如下条件旋转或平移后的图形:1)以B点为旋转中心,按逆时针方向旋转30°;2)以B点为旋转中心,按逆时针方向旋转180°;3)取三角形外一点P为旋转中心,按逆时针方向旋转180°;4)将△ABC平移,使得B点的对应点为A点。
已知两个共用一个顶点的等腰Rt△ABC,等腰Rt△CEF,∠ABC=∠CEF= 90o,连接AF,M是AF的中点,连接MB,ME。 (1)如图1,当CB与CE在同一直线上时,若CB=a,CE=2a,求BM,ME的长; (2)如图2,当∠BCE=45o时,求证:BM=ME。
如图所示,一焦距为 的凸透镜,主轴和x轴重合。x轴上有一光点位于透镜的左侧,光点到透镜的距离在 和2 之间。若将此透镜沿戈轴向右缓慢平移2 的距离,则在此过程中,光点经透镜所成的像点将( )。A.一直向右移动 B.一直向左移动 C.先向左移动.接着向右移动 D.先向右移动,接着向左移动
如图所示,一焦距为f的凸透镜,主轴和x轴重合。x轴上有一光点位于透镜的左侧,光点到透镜的距离在f和2f之间。若将此透镜沿x轴向右缓慢平移2f的距离,则在此过程中,光点经透镜所成的像点将( )。 A.一直向右移动B.一直向左移动C.先向左移动.接着向右移动D.先向右移动.接着向左移动
小学数学《平移》一、考题回顾二、考题解析【教学过程】(一)导入新课老师做关窗、拉黑板的动作。提问:同学们,你们知道这些是什么现象吗? 引导学生说出:这是平移现象。追问:你还能说出生活中有哪些关于平移的现象?学生答:升旗,缆车,火车在笔直的铁轨上开等。(二)生成新知(1)课件出示教材中的例题1图。先让学生说出虚线部分和实线部分表示的是什么意思。提出问题:下面的小船图和金鱼图分别是怎样运动的?它们的运动有什么相同点和不同点?(2)教师动画演示小船图和金鱼图运动的过程,让学生观察,感受平移,并强调平移的方向。提问:小船图和金鱼图都进行了平移,它们是朝哪个方向平移的呢?学生观察得出:小船图和金鱼图都是向右平移。讲解概念:(1)认识平移的距离。提问:小船图和金鱼图都是向右平移,它们的运动有什么不同吗?引导学生发现:小船图平移的距离比金鱼图远一些,并数一数。(引导:数一数,小船图向右平移了几格?)小组交流讨论,教师巡视,进行纠错。之后组织全班交流。师质疑:有位同学数出两艘小船之间的距离是4格,他认为平移的距离就是4格,你觉得对吗?引导学生得出:4格只是两艘小船之间的距离,而不是小船平移的距离。追问:刚才同学们在小组内交流了怎样数平移了几格的方法,谁来和大家分享一下,你是怎么数的?引导学生进行汇报交流,学生可能会出现不同的数法,教师可以组织全班同学进行评价和判断,必要时让学生上台演示自己数的方法。数法预设:方法一:看船帆上的一条线段,这条线段向右平移了9格,小船图就向右平移9格。方法二:看船头的一个点,这个点向右平移了9格,小船图就向右平移9格。(2)数一数:金鱼图向右平移了几格?再与同学交流。 先让学生独立完成,再组织交流,教师巡视。(3)小结确定平移的距离的方法。先让学生说说,教师再结合学生的发言进行小结:我们在确定图形平移的距离时,可以先找出参照点,看它向哪个方向平移了几格,这个图形就向那个方向平移了几格。(三)应用新知完成教材中的“试一试”。(1)学生独立画图。教师巡视,了解学生存在的问题,对个别有困难的学生进行适当辅导。(2)组织汇报。学生一边用投影展示画出的图形,一边汇报是怎么画的。师根据学生的汇报小结画法:一种方法是先确定平行四边形的四个顶点,找出每个顶点平移后的对应点,再将这四个对应点依次连接起来;另一种方法是找每条边平移后的对应边。(四)小结作业小结:通过这节课的学习,你有什么收获?你对今天的学习还有什么疑问吗?作业:想一想,生活中还有哪些是平移的现象?【板书设计】【答辩题目解析】1.在本节课的教学过程中,你是如何引导同学们正确画出平移后的图形?2.教材中为什么要采用方格图?
A.向左平移2个单位长度,再向上平移2个单位长度B.向右平移2个单位长度,再向上平移2个单位长度C.向左平移2个单位长度,再向下平移2个单位长度D.向右平移2个单位长度,再向下平移2个单位长度
单选题在IS-LM模型中,增加已经退休人员的养老金的后果是()。AIS曲线向右平移BLM曲线向右平移CIS曲线向左平移DLM曲线向左平移