如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。 A.12B.14C.15D.16
如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。
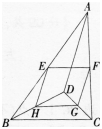

A.12
B.14
C.15
D.16
B.14
C.15
D.16
参考解析
解析:因为BD⊥CD,BD=8,CD=6,由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=


相关考题:
对边相等,对角相等的凸四边形,是平行四边形吧? 方法①∠B小于90°;左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:过A作AN⊥BC于N;过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法②∠B大于90°左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:延长CD,过A作AN⊥BC于N;延长AB,过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法③∠B等于90°证明:∵∠B=∠D=90°;AB=CD;AC=AC∴△ABC=△ADC(HL)∴AB=CB∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。有错吗?若我的证明有错请明示,我知道有个反例,但它是凹四边形。
如右图所示,在△ABC:中,D为AC的中点,E在BC上,且 BE : EC=1 : 2,AE与BD交于F。则△BEF与四边形EFDC 的面积之比为( )。A. 1 : 3 B. 1 : 4C. 1 : 5 D. 1 : 6
从建筑群设备间到工作区,综合布线系统正确的顺序是()A、CD——FD——BD——TO——CP——TEB、BD——CD——FD——TO——CP——TEC、CD——BD——FD——CP——TO——TED、BD——CD——FD——CP——TO——TE
单选题直径为d的圆形对其形心轴的惯性半径i等于:()Ad/2Bd/4Cd/6Dd/8