设总体X的密度函数为f(x)=,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.
设总体X的密度函数为f(x)=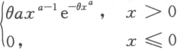
,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.
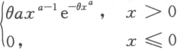,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.参考解析
解析：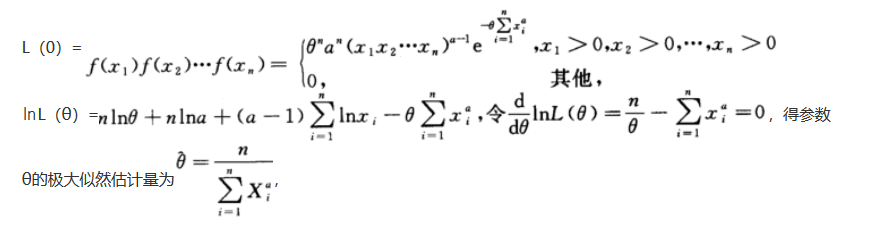
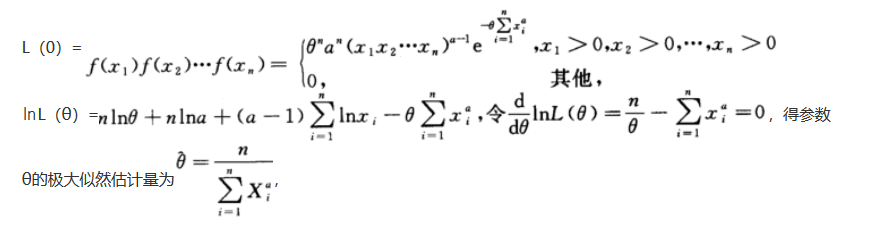
相关考题：
设总体X的分布函数为其中θ是未知参数且大于零.X1，X2，…，Xn为来自总体X的简单随机样本. (Ⅰ)求EX与EX^2； (Ⅱ)求θ的最大似然估计量. (Ⅲ)是否存在实数a，使得对任何ε>0，都有？
设总体X的概率分布为 其中参数θ∈(0，1)未知.以Ni表示来自总体X的简单随机样本(样本容量为n)中等于i的个数(i=1，2，3).试求常数α1，α2，α3，使为θ的无偏估计量，并求T的方差.
设总体X的概率密度为其中θ∈(0,+∞)为未知参数，X1，X2，X3为来自总体X的简单随机样本，令T=max(X1，X2，X3). (Ⅰ)求T的概率密度； (Ⅱ)确定a，使得aT为θ的无偏估计.
单选题设总体X服从参数为λ的泊松分布，其中λ未知．X1，…，X是取自总体X的样本，则A的最大似然估计是（）．AXBS2CSD2