窄带噪声n(t)的同相分量nc(t)与正交分量ns(t)具有如下性质:()。 A、都具有低通性质B、都具有带通性质C、都具有带阻性质D、都具有高通性质
如果一个矩阵的行向量组为正交的单位向量组且为方阵,那么这个矩阵的行列式为1。() 此题为判断题(对，错)。
下述结论中,不正确的有() A.若向量a与β正交，则对任意实数a,b,aα与bβ也正交B.若向量β与向量a1,a2都正交，则β与a1,a2的任一线性组合也正交C.若向量a与正交，则a,β中至少有一个是零向量D.若向量a与任意同维向量正交，则a是零向量.
设α=i+k，β=-j+k，与α，β都垂直的单位向量为( )。A.±(i+j-k)B.C.D.
设α=i+2j+3k，β=i-3j-2k，与α、β都垂直的单位向量为( )。A.±(i+j-k)B.C.D.
设α=i+2j+3k，β=i-3j-2k，则与α，β 都垂直的单位向量为：
已知两点A(4，0，5)和B(7，1，3)，则下面与AB方向相同的单位向量e为( )。
已知二次型可用正交变换化为.求a,并且作实现此转化的正交变换
设二次型 (b>0), 其中二次型的矩阵A的特征值之和为1，特征值之积为-12. (1)求a，b的值； (2)利用正交变换将二次型f化为标准形，并写出所用的正交变换和对应的正交矩阵.
已知二次型经过正交变换化为标准型，求参数a,b及所用的正交变换矩阵
设二次型其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型化成标准型(需写出正交变换及标准型)
设α=i+2j+3k,β=i-3j-2k,与α、β都垂直的单位向量为（ ）。
将一个函数通过正交分解映射到正交函数空间的数学变换称为（）。
X为3阶随机矩阵，分别对X进行如下操作： 求X的三角分解；求X的正交分解；求X的特征值分解；求X的奇异值分解；
正交和极轴追踪是（）。A、不同的概念B、名称不同，但是一个概念C、极轴是正交的一个特例D、正交是极轴追踪的一个特例
直流电机的交轴电枢反应中，电枢磁势的轴线（）.A、与几何中性线正交。B、与物理中性线正交。C、与磁感应线正交。D、与主极轴线正交。
问答题X为3阶随机矩阵，分别对X进行如下操作： 求X的三角分解；求X的正交分解；求X的特征值分解；求X的奇异值分解；
单选题正交和极轴追踪是（）。A不同的概念B名称不同，但是一个概念C极轴是正交的一个特例D正交是极轴追踪的一个特例
填空题将一个函数通过正交分解映射到正交函数空间的数学变换称为（）。
填空题如果一条直线与一个平面垂直，那么称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是____．
，
，
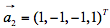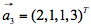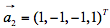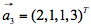都正交的单位向量
