证明:线性方程组有解的充要条件是.
证明:线性方程组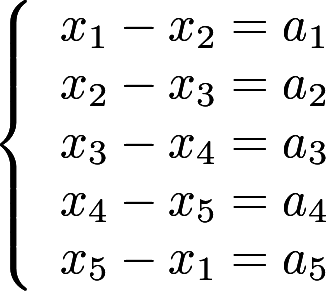 有解的充要条件是.
有解的充要条件是.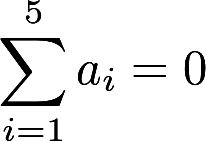
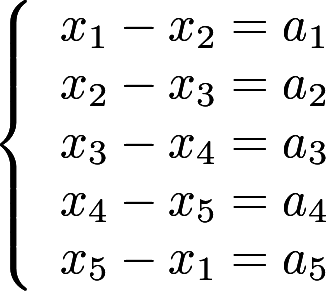 有解的充要条件是.
有解的充要条件是.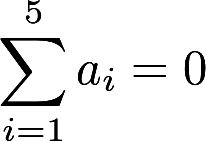
参考解析
解析:

相关考题:
设A为n阶方阵,r(A)n,下列关于齐次线性方程组Ax=0的叙述正确的是() A、Ax=0只有零解B、Ax=0的基础解系含r(A)个解向量C、Ax=0的基础解系含n-r(A)个解向量D、Ax=0没有解
设非齐次线性方程组( I )的导出方程组为(II),则()。A.当(I )只有唯一 解时,(II)只有零解B. (I )有解的充分必要条件是(II)有解C.当(I )有非零解时,(II)有无穷多解D.当(I)有非零解时,(I )有无穷多解
单选题n元线性方程组AX(→)=b(→)有唯一解的充要条件为( )。AA为方阵且|A|≠0B导出组AX(→)=0(→)仅有零解C秩(A)=nD系数矩阵A的列向量组线性无关,且常数向量b(→)与A的列向量组线性相关
单选题第一个证明高于四次的方程可用根式求解的充要条件的人是()。A鲁布尼B阿贝尔C拉格朗日D伽罗瓦