已知线性方程组AX=Kβ1+β2有解,其中等于( )。A、1B、-lC、2 D、-2
已知线性方程组AX=Kβ1+β2有解,其中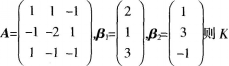
等于( )。
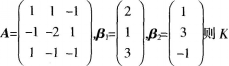
等于( )。
A、1
B、-l
C、2
D、-2
B、-l
C、2
D、-2
参考解析
解析:已知线性方程组是非齐次的,如果方程要有解,则系数矩阵的秩要等于增广矩阵的秩.由此可以求出K。 

相关考题:
设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是() A、η1+η2是Ax=0的一个解B、(1/2)η1+(1/2)η2是Ax=b的一个解C、η1-η2是Ax=0的一个解D、2η1-η2是Ax=b的一个解
设A为n阶方阵,r(A)n,下列关于齐次线性方程组Ax=0的叙述正确的是() A、Ax=0只有零解B、Ax=0的基础解系含r(A)个解向量C、Ax=0的基础解系含n-r(A)个解向量D、Ax=0没有解
设A是4×5矩阵,ξ1,ξ2是齐次线性方程组Ax=0的基础解系,则下列结论正确的是( ).A.ξ1-ξ2,ξ1+2ξ2也是Ax=0的基础解系B.k1ξ1+k1ξ2是Ax=0的通解C.k1ξ1+ξ2是Ax=0的通解D.ξ1-ξ2,ξ2-ξ1也是Ax=0的基础解系
已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3,且η1,η2,η3是3个不同的解向量,则通解是( ).A.x=k1(η-η2)+η3B.x=k1η1+k2η2+η3C.x=k1η1+k2η2+k3η3D.x=k1(η+η2)+η3
单选题设n阶矩阵A的各行元素之和均为零,且A的秩为n-1,则线性方程组AX(→)=0(→)的通解为( )。AX(→)=k(1,1,…,1)TBX(→)=k(1,1,…,-1)TCX(→)=k(-1,1,…,1)TDX(→)=k(-1,1,…,-1)T
单选题已知β(→)1β(→)2是非齐次方程组AX(→)=b(→)的两个不同的解,α(→)1α(→)2是其对应的齐次线性方程组的基础解系,k1、k2是任意常数,则方程组AX(→)=b(→)的通解必是( )。Ak1α(→)1+k2(α(→)1+α(→)2)+(β(→)1-β(→)2)/2Bk1α(→)1+k2(α(→)1-α(→)2)+(β(→)1+β(→)2)/2Ck1α(→)1+k2(β(→)1+β(→)2)+(β(→)1-β(→)2)/2Dk1α(→)1+k2(β(→)1-β(→)2)+(β(→)1+β(→)2)/2
填空题已知四元非齐次方程组AX(→)=b(→),r(A)=3,α(→)1,α(→)2,α(→)3是它的三个解向量,且α(→)1+α(→)2=(1,1,0,2)T,α(→)2+α(→)3=(l,0,1,3)T,则AX(→)=b(→)的通解是____。
单选题设α(→)1,α(→)2,α(→)3,α(→)4是4维非零列向量组,A=(α(→)1,α(→)2,α(→)3,α(→)4),A*是A的伴随矩阵,已知方程组AX(→)=0(→)的基础解系为k(1,0,2,0)T,则方程组A*X(→)=0(→)的基础解系为( )。Aα(→)1,α(→)2,α(→)3Bα(→)1+α(→)2,α(→)2+α(→)3,3α(→)3Cα(→)2,α(→)3,α(→)4Dα(→)1+α(→)2,α(→)2+α(→)3,α(→)3+α(→)4,α(→)4+α(→)1
单选题设β1,β2是线性方程组Ax=b的两个不同的解,α1、α2是导出组Ax=0的基础解系,k1、k2是任意常数,则Ax=b的通解是( )。A(β1-β2)/2+k1α1+k2(α1-α2)Bα1+k1(β1-β2)+k2(α1-α2)C(β1+β2)/2+k1α1+k2(α1-α2)D(β1+β2)/2+k1α1+k2(β1-β2)
问答题已知m个向量α(→)1,α(→)2,…,α(→)m线性相关,但其中任意m-1个都线性无关,证明: (1)如果存在等式k1α(→)1+…+kmα(→)m=0(→),则这些系数k1,…,km或者全为零,或者全不为零。 (2)如果存在两个等式k1α(→)1+…+kmα(→)m=0(→),l1α(→)1+…+lmα(→)m=0(→),其中l1≠0,则k1/l1=k2/l2=…=km/lm。
单选题已知n元非齐次线性方程组Ax=B,秩r(A)=n-2,α1,α2,α3为其线性无关的解向量,k1,k2为任意常数,则Ax=B的通解为( )。[2014年真题]Ax=k1(α1-α2)+k2(α1+α3)+α1Bx=k1(α1-α3)+k2(α2+α3)+α1Cx=k1(α2-α1)+k2(α2-α3)+α1Dx=k1(α2-α3)+k2(α1+α2)+α1
单选题非齐次线性方程组AX(→)=b(→)中未知数个数为n,方程个数为m,系数矩阵A的秩为r,则( )。Ar=m时,方程组AX(→)=b(→)有解Br=n时,方程组AX(→)=b(→)有唯一解Cm=n时,方程组AX(→)=b(→)有唯一解Dr<n时,方程组AX(→)=b(→)有无穷多解
单选题设n元齐次线性方程组AX(→)=0(→),秩(A)=n-3,且α(→)1,α(→)2,α(→)3为其3个线性无关的解,则( )为其基础解系。Aα(→)1+α(→)2,α(→)2+α(→)3,α(→)1+α(→)3Bα(→)1-α(→)2,α(→)2-α(→)3,α(→)3-α(→)1Cα(→)1+α(→)2+α(→)3,α(→)3-α(→)2,α(→)1+2α(→)3Dα(→)1-α(→)2,2α(→)2-3α(→)3,3α(→)3-2α(→)1