设A,B都是n阶对称阵,证明AB是对称阵的充要条件是AB=BA.

设A,B都是n阶对称阵,证明AB是对称阵的充要条件是AB=BA.

参考解析

解析：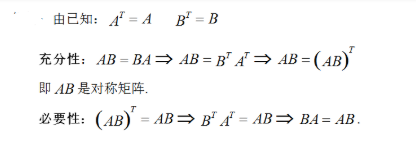

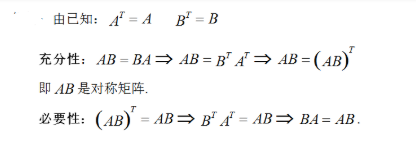
相关考题：

可对角化的矩阵是____。 A.实对称阵B.有n个相异特征值的n阶阵C.有n个线性无关的特征向量的n阶方阵
查看答案
若A,B均为对称阵,则AB＋BA也是对称阵。() 此题为判断题(对，错)。
查看答案
设A,B均为n阶非零方阵,下列选项正确的是() A. (A+B)(A-B) = A^2-B^2B. (AB)^-1 = B^-1A^-1C. 若AB= O, 则A=O或B=OD. |AB| = |A| |B|
查看答案
设A,B,C均为n阶非零方阵,下列选项正确的是()。 A、若AB=AC，则B=CB、(A-C)^2=A^2-2AC+C^2C、ABC=BCAD、|ABC|=|A||B||C|
查看答案
设A,B是正定实对称矩阵，则().A. AB,A+B一定都是正定实对称矩阵B. AB是正定实对称矩阵，A+B不是正定实对称矩阵C. A+B是正定实对称矩阵，AB不一定是正定实对称矩阵D. AB必不是正定实对称矩阵，A+B必是正定实对称矩阵
查看答案
设A,B为n阶对称矩阵,下列结论不正确的是().A.AB为对称矩阵B.设A,B可逆,则A^-1+B^-1为对称矩阵C.A+B为对称矩阵D.kA为对称矩阵
查看答案
已知n阶非零方阵A，B满足条件AB=O，则下列结论正确的是（ ）。
查看答案
设A为n阶实对称矩阵,下列结论不正确的是().A.矩阵A与单位矩阵E合同B.矩阵A的特征值都是实数C.存在可逆矩阵P,使P^-1AP为对角阵D.存在正交阵Q,使Q^TAQ为对角阵
查看答案
设A是3阶方阵，A能与对角阵相似的充分必要条件是( ).A.B.A是实对称阵C.A有3个线性无关的特征向量D.A有3个不同的特征值
查看答案
设A与B都是n阶方阵,且,证明AB与BA相似.
查看答案
设A,B为n阶矩阵.　　(1)是否有AB～BA；(2)若A有特征值1,2,…,n,证明：AB～BA.
查看答案
设A是nxm矩阵，B是mxn矩阵，E是n阶单位阵，若AB=E，证明B的列向量组线性无关。
查看答案
设A,B都是N阶对称矩阵，证明AB是对称矩阵的充分必要条件是.AB=BA
查看答案
设x为n维列向量,,令,证明H是对称的正交阵.
查看答案
设，求一秩为2的3阶方阵B使AB=0
查看答案
设A，B都是n阶矩阵，AB+E可逆．证明BA+E也可逆，并且．
查看答案
设A、B都是n阶方阵，满足AB=A-B，请证明：AB=BA
查看答案
设A和B都是n阶矩阵.记,. (1)求HG和GH. (2)证明|E-AB|=|E-BA|.
查看答案
设A，B是n阶方阵，下列命题正确的是（）．A、若A，B都是可逆阵，则A+B也是可逆阵B、若A+B是可逆阵，则A、B中至少有一个是可逆阵C、若AB不是可逆阵，则A、B也都不是可逆阵D、若ATA=E，则
查看答案
设A，B是n阶对称阵，Λ是对角阵，下列矩阵中不是对称阵的是（）．A、A+2EB、A+ΛC、ABD、A-B
查看答案
设A是n阶方阵（不一定是对称阵）．二次型f（x）=xTAx相对应的对称阵是（）．A、AB、ATC、1/2（A+AT）D、A+AT
查看答案
设A是3阶方阵，A能与对角阵相似的充分必要条件是（）．A、存在可逆阵P，使得P-1AP=BB、A是实对称阵C、A有3个线性无关的特征向量D、A有3个不同的特征值
查看答案
填空题设A、B都是4阶方阵且AB＝0，则r（A）＋r（B）____。
查看答案
单选题设A，B是n阶方阵，下列命题正确的是（）．A若A，B都是可逆阵，则A+B也是可逆阵B若A+B是可逆阵，则A、B中至少有一个是可逆阵C若AB不是可逆阵，则A、B也都不是可逆阵D若ATA=E，则
查看答案
单选题设A是n阶方阵（不一定是对称阵）．二次型f（x）=xTAx相对应的对称阵是（）．AABATC1/2（A+AT）DA+AT
查看答案
单选题设A，B是n阶对称阵，Λ是对角阵，下列矩阵中不是对称阵的是（）．AA+2EBA+ΛCABDA-B
查看答案
单选题设A、B都是4阶方阵且AB＝0，则r（A）＋r（B）（　　）。A≤1B≤2C≤3D≤4
查看答案
热门标签