设随机变量X和Y相互独立,且都服从标准正态分布,则:P(X+Y≥0)=()。
设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X+Y服从的分布为() A、X+Y服从N(0,1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布
设两个相互独立的随机变量X和Y分别服从正态分布N(0,1)和N(1,1),则
设随机变量X~N(μ,σ^2),且方程x^2+4r+X=0无实根的概率为,则μ=_______.
设二维随机变量(X,Y)服从二维正态分布,且X~N(1,3^2),Y~N(0,4^2),且X,Y的相 关系数为-,又设Z=(1)求E(Z),D(Z);(2)求;(3)X,Z是否相互独立?为什么?
设随机变量X~N(0,1),且y=9X^2,则y的密度函数为_______.
设随机变量X,Y相互独立且都服从二项分布B(n,p),则P{min(X,Y)=0}=_______.
设随机变量X~N(0,σ^2),Y~N(0,4σ^2),且P(X≤1,y≤-2)=,则P(X>1,Y>-2)=_______.
设二维随机变量(X,Y)服从正态分布N(μ,μ;σ^2,σ^2;0),则E(XY^2)=________.
设二维随机变量(X,Y)服从正态分布N(1,0;1,1;0),则P{XY-Y
设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y的概率分布为P{Y=0}=P{Y=1}=.记Fz(z)为随机变量Z=XY的分布函数,则函数Fz(z)的间断点个数为 A.A0B.1C.2D.3
设随机变量X和Y相互独立,都服从正态分布N(μ,σ2),令ξ=X+Y,η=X−Y,则ξ和η的相关系数为()。A、-4/9B、-1/2C、1/2D、0E、5/9
设随机变量X服从正态分布N(μ,σ2)(其中σ0),则随着的σ增大,概率P{|X-μ|σ}()。A、单调增大B、单调减小C、保持不变D、增减不定
设随机变量X和Y相互独立,都服从正态分布N(0,1/2),则Y−X的方差为()。A、1-1/πB、1-2/πC、1D、2E、4
设随机变量X和Y都服从N(0,1)分布,则下列叙述中正确的是()。A、X+Y服从正态分布B、X2+Y2~x2分布C、X2和Y2都服从X2分布D、分布
设随机变量X服从正态分布N(μ1,σ21),随机变量Y服从正态分布N(μ2,σ22),且P{|X-μ1|1}P{|Y-μ2|1},则必有()A、σ1σ2B、σ1σ2C、μ1μ2D、μ1μ2
设二维随机变量(X,Y)在区域D上服从均匀分布,其中D://0≤x≤2,0≤y≤2。记(X,Y)的概率密度为f(x,y),则f(1,1)=()
设X服从0—1分布,P=0.6,Y服从λ=2的泊松分布,且X,Y独立,则X+Y().A、服从泊松分布B、仍是离散型随机变量C、为二维随机向量D、取值为0的概率为0
若随机变量X服从正态分布N(0,4),则随机变量Y=X-2的分布为()A、N(-2,4)B、N(2,4)C、N(0,2)D、N(-2,2)
如果随机变量X和Y服从联合正态分布,且X与Y的协方差为0,则X与Y相互独立。
设(X,Y)服从二元正态分布N(0,1,1,4,0,5),则E(2X2-XY+3)=()。
设X,Y相互独立,且都服从标准正态分布N(0,1),令Z=X2+Y2则Z服从的分布是().A、N(0,2)分布B、单位圆上的均匀分布C、参数为1的瑞利分布D、N(0,1)分布
设随机变量X服从正态分布U(μ,σ2)(σ0),且二次方程y2+4y+X=0无实根的概率为1/2,则μ=()
单选题若随机变量X服从正态分布N(0,4),则随机变量Y=X-2的分布为()AN(-2,4)BN(2,4)CN(0,2)DN(-2,2)
填空题设随机变量X服从正态分布N(μ,σ2)(σ>0),且二次方程y2+4y+X=0无实根的概率为0.5,则μ=____。
单选题设随机变量X和Y相互独立,都服从正态分布N(0,1/2),则Y−X的方差为()。A1-1/πB1-2/πC1D2E4
单选题设随机变量X服从正态分布N(μ,σ2)(σ>0),且二次方程y2+4y+X=0无实根的概率为0.5,则μ=( )。A1B2C4D5
 ,则μ=________.
,则μ=________. ,则μ=________.
,则μ=________. ,即P{X>4}=
,即P{X>4}=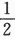 ,所以μ=4,答案应填4.
,所以μ=4,答案应填4.
 ,即P{X>4}=
,即P{X>4}=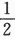 ,所以μ=4,答案应填4.
,所以μ=4,答案应填4.