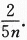设X1,X2,…,Xn是来自总体的样本,且EX=μ,DX=б2则()是μ的无偏估计。
设X1,X2,…,X16是来自总体X~N(4,б2)的简单随机样本,б2已知,令,则统计量服从的概率密度函数为()
设总体X~N(2,42),(x1,x2,…,Xn)是来自X的简单随机样本,则下面结果正确的是( )。A.B.C.D.
设(X1,X2,…,Xn)是来自正态总体N(μ,σ2)的简单随机样本,其中参数μ,σ2未知,则下列各项中,不是统计量的有( )。
设(X1,X2,…,Xn)(N≥2)为标准正态总体X的简单随机样本,则().
设总体X的概率密度为未知参数,X1,X2, ...Xn是来自总体X的样本,则θ的矩估计量是:
设总体X的概率密度为而x1,x2,...,xn 是来自总体的样本值,则未知参数θ的最大似然估计值是:
设总体X的概率密度为f(x)=其中θ>-1是未知参数,X1,X2,...Xn是来自总体X的样本,则θ的矩估计量是:
设某元件的使用寿命X的概率密度为f(x;θ)=,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.
设总体X服从参数为2的指数分布,X1,X2,…,Xn为来自总体X的简单随机样本,则当n→∞时,依概率收敛于_______.
设总体X的分布函数为 其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求: (Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.
设总体X的分布律为P(X=k)P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
设总体X,Y相互独立且都服从N(μ,σ^2)分布,(X1,X2,…,Xn)与(Y1,Y1,…,yn)分别为来自总体X,Y的简单随机样本,证明:为参数σ^2的无偏估计量,
设总体X的分布律为P(X=i)=(i=1,2,…,θ,X1,X2,…,Xn为来自总体的简单随机样本,则θ的矩估计量为_______(其中θ为正整数).
设总体X的密度函数为f(x)=,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.
设x为一个总体且E(x)=k,D(x)=1,X1,X2,…,xn为来自总体的简单随机样本,令,问n多大时才能使P?
设总体X的密度函数为f(x)=,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ;(2)求D(θ).
设总体X的概率密度为f(x)=,其中θ>-1是未知参数,X1, X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.
设总体X的概率密度为f(x)=,其中未知参数θ>0,设X1,X2,…,X是来自总体X的简单样本.(1)求θ的最大似然估计量;(2)该估计量是否是无偏估计量?说明理由.
设x为总体,E(X)=μ,D(x)=σ^2,X1,X2,…,xn为来自总体的简单随机样本,S^2=,则E(S^2)=_______.
设总体X的分布函数为其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本. (Ⅰ)求EX与EX^2; (Ⅱ)求θ的最大似然估计量. (Ⅲ)是否存在实数a,使得对任何ε>0,都有?
设总体X的概率密度为 其中参数λ(λ>0)未知,X1,X2,…,Xn是来自总体X的简单随机样本.(Ⅰ)求参数λ的矩估计量;(Ⅱ)求参数λ的最大似然估计量.
设总体X的概率密度为 其中μ是已知参数,σ>0是未知参数,A是常数.X1,X2,…,Xn是来自总体X的简单随机样本. (Ⅰ)求A; (Ⅱ)求σ的最大似然估计量.
设总体X的概率密度为 其中θ为未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本. (Ⅰ)求θ的矩估计量; (Ⅱ)求θ的最大似然估计量.
设总体X的概率密度为 其中θ为未知参数,X1,X2,…,Xn,为来自该总体的简单随机样本. (Ⅰ)求θ的矩估计量; (Ⅱ)求θ的最大似然估计量.
设总体X的概率密度为其中θ∈(0,+∞)为未知参数,X1,X2,X3为来自总体X的简单随机样本,令T=max(X1,X2,X3). (Ⅰ)求T的概率密度; (Ⅱ)确定a,使得aT为θ的无偏估计.
设总体X~N(μ,σ2),X1,X2,X3为来自该总体的一组简单随机样本,假设是未知参数μ的无偏估计,则α=()A、1/2B、1/3C、1/4D、1/5
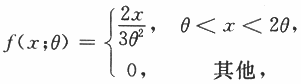 其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若
其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若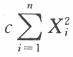 是θ的无偏估计,则c=______.
是θ的无偏估计,则c=______.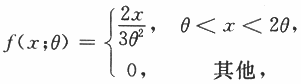 其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若
其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若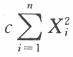 是θ的无偏估计,则c=______.
是θ的无偏估计,则c=______. 答案应填.
答案应填.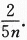
 答案应填.
答案应填.