在一元线性回归中，给出n对数据(xi,yi), i =1， 2，…n，若其回归方程为，则下述结论不成立的有（ ）。A.总偏差平方和ST=Lyy B.回归平方和SR=bxLxyC.残差平方和SE=ST-SR D.残差平方和的自由度为n-1
在一元线性回归中，给出n对数据(xi,yi), i =1， 2，…n，若其回归方程为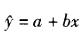
，则下述结论不成立的有（ ）。
A.总偏差平方和ST=Lyy B.回归平方和SR=bxLxy
C.残差平方和SE=ST-SR D.残差平方和的自由度为n-1
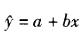，则下述结论不成立的有（ ）。
A.总偏差平方和ST=Lyy B.回归平方和SR=bxLxy
C.残差平方和SE=ST-SR D.残差平方和的自由度为n-1
参考解析
解析：总偏差平方和的自由度fT=n-1，回归平方和的自由度fR =1，所以残差平方和的自由度fE =fT-fR = n -2。
相关考题：
收集了n组数据(xi，yi)，i=1，2，…，n，在一元线性回归中用SR表示回归平方和，SE表示残差平方和，由此求得F比，则当( )时在显著性水平α上认为所得到的回归方程是有意义的。A．F＞F1-α(1，n)B．F＞F1-α(1，n-1)C．F＞F1-α(1，n-2)D．F＜F1-α(1，n-2)
两个变量(x，y)，其观测值为(xi，yi)，i=1，2，…，n。当相关系数的绝对值｜r｜大于某个临界值时，就认为它们之间存在一定的线性相关关系。若给定显著水平α，则临界值为( )。A．r1-α(n-1)B．r1-α/2(n-1)C．r1-α(n-2)D．r1-α/2(n-2)
有n对变量值(Xi,yi)建立直线回归方程,要求A.使∑(Xi一xi)最小 B.使∑(Xi—yi)2最小 S 有n对变量值(Xi，yi)建立直线回归方程，要求A.使∑(Xi一xi)最小B.使∑(Xi—yi)2最小C.使∑(yi—Yi)2最小D.使∑(Xi一xi)2最小E.使∑(yi—yi)2最小
在一元线性回归中，给出n对数据(xi，yi)，i=1，2，…，n，若其回归方程为bx，则下述结论不成立的有( )。A．总偏差平方和ST=LyyB．回归平方和SR=b×LxyC．残差平方和SE=ST-SRD．残差平方和的自由度为n-1
在一元线性回归中，给出n对数据(xi，yi)，i=1，2，…，n，若其回归方程为bx，则下述结论成立的有( )。A．总离差平方和ST=LyyB．回归平方和SR=bLxyC．残差平方和SE=ST-SR)D．残差平方和的自由度为n-1E．残差平方和Se=ST-Sf
在一元线性回归中，给出n对数据(xi，yi)，i=1，2…，n，若其回归方程为，则下述结论成立的有( )。A．总偏差平方和ST＝LyyB．归平方和SR＝bLxyC．残差平方和Se＝ST-SRD．残差平方和的自由度为n-1E．残差平方和Se＝ST-Sf
设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布
若收集了n组数据(xi，yi)，i=1，2，…，n，并求得Lxx=330，Lxy=168，如Lyy= 88.9，则一元线性回归方程(作图)中的b=( )。A．0.5091B．0.5292C．1.8898D．1.9643
设Xi (i=1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。A．若Xi (i=1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布B．若Xi (i=1，2，…，n)服从指数分布，且λ相同，则服从正态分布C．若Xi(i=1，2，…，n)服从[a，b)上的均匀分布，则服从正态分布D．无论Xi (i=1，2，…，n)服从何种分布，其均值都服从正态分布
若收集了n组数据(xi,yi), i =1， 2，…n，并求得Lxx=330，Lxy=168，Lyy=88.9，则一元线性回归方程中的b=( )。A. 0.5091 B. 0.5292 C. 1. 8898 D. 1.9643
两个变量(X，Y),其观测值(xi,yi), i =1， 2，…n，若显著性水平为a，相关系数为r，则下列说法正确的有（ ）。A. -1≤r≤1B. r=0,x, y间存在线性相关C. r= -1,完全负线性相关D.相关系数检验的临界值表示为r1-a/2(n-2)E. r=0, x,y可能存在某种函数关系
设两变量X和Y的观测值为(xi,yi), i =1， 2，…n，用r表示相关系数，表示回归方程，以下结论正确的有（ ）。A.若r= 1,则b= 1 B.若rC.若r=0,则b=0 D.若r>0,则b>0E.若r= 1,则a = 0
设两变量X与Y的观测值为(xi,yi)，i= 1，2，…，n,用r表示相关系数，y = a + bc表示回归方程，以下结论正确的有（ ）。A.若 r=1，则b=1 B.若 rC.若 r=0，则b= 0 D.若r>0，则b>0E.若 r = 1，则 a = 0
设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求： (1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).
若收集了n组数据(Xi，Yi)(i=1，2，…，n)，求得两个变量间的相关系数为1，则下列说法正确的是（）。A、两个变量独立B、两个变量间完全线性相关C、两个变量问一定有函数关系D、两个变量间呈负相关
一元线性回归模型Yi=β0+β1Xi+μi的最小二乘回归结果显示，残差平方和RSS=40.32，样本容量n=25，则回归模型的标准差σ为（）。A、1.270B、1.324C、1.613D、1.753
一元线性回归模型Yi=β0+β1Xi+μi的基本假定包括（）。A、E（μi）=0B、Var（μi）=σ2C、Cov（μi，μj）（i≠j）D、μi～N（0，1）E、X为非随机变量，且Cov（Xiμi）=0
通过最小二乘估计，得到某地区某种钢板消费量(Y)与同期第二产业产值(X)的一元线性回归方程为y=-7.55+9.59x，经计算∑(yi-yi’)2=11.87，∑(xi-x)2=1.56，取α=0.05，对其进行t检验，结论是（ ）。(已知t(0.05,8)=1.86;t(0.025,8)=2.36，n=10)A、tb大于1.86，线性假设合理B、tb大于1.86，线性假设不合理C、tb大于2.36，线性假设合理D、tb大于2.36，线性假设不合理
单选题在对两个变量x，y进行线性回归分析时，有下列步骤： ①对所求出的回归直线方程作出解释； ②收集数据（xi，yi），1，i=2，…，n； ③求线性回归方程； ④求未知参数； ⑤根据所搜集的数据绘制散点图 如果根据可行性要求能够作出变量x，y具有线性相关结论，则在下列操作中正确的是（）A①②⑤③④B③②④⑤①C②④③①⑤D②⑤④③①
单选题收集了n组数据(Xi，Yi)，i=1，2，…，n，画出散布图，若n个点基本在一条直线附近时，称两个变量具有( )。A独立关系B不相容关系C函数关系D线性相关关系