函数f(x)= 10arctanx-3lnx的极大值是:
函数f(x)= 10arctanx-3lnx的极大值是:
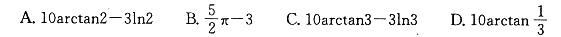
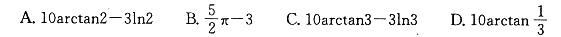
参考解析
解析:提示:函数的定义域(0,+∞),求驻点,用驻点分割定义域,确定极大值。计算如下:
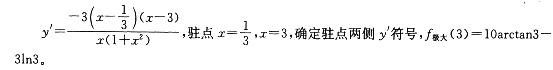
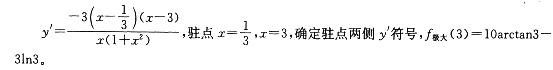
相关考题:
● 某一类应用问题中,需要求正比例函数与反比例函数之和的极值。例如,正比例函数 4x 与反比例函数 9/x 之和用 f(x)表示, 即 f(x)=4x + 9/x, (x0) ,那么函数 f(x) (63) 。(63)A. 没有极小值B. 在 x=1 时达到极大值C. 在 4x=9/x 时达到极小值D. 极大值是极小值的 9/4 倍
设函数f(x)在内连续,其导函数的图形如图所示,则f(x)有(52)。A.一个极小值点和两个极大值点B.两个极小值点和一个极大值点C.两个极小值点和两个极大值点D.三个极小值点和一个极大值点
设f(x)是(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论( )。A.f(0)是f(x)在(-a,a)的极大值,但不是最大值B.f(0)是f(x)在(-a,a)的最小值C.f(0)是f(x)在(-a,a)的极大值,也是最大值D.f(0)是曲线y=f(x)的拐点的纵坐标
设函数f(x)在x=a的某个邻域内连续,且f(a)为其极大值,则存在δ>0,当x∈(a-δ,a+δ)时,必有( )。A.(x-a)[f(x)-f(a)]≥0B.(x-a)[f(x)-f(a)]≤0C.D.
根据f(x)的导函数f'(x)的图像,判定下列结论正确的是()A.在(-∞,-1)内,f(x)是单调增加的B.在(-∞,0)内,f(x)是单调增加的C.f(-1)为极大值D.f(-1)为极小值
设函数y-f(x)连续,除x=a外f''(x)均存在。一一阶导函数y'=f(x)的图形如下,则y=f(x)A.有两个极大值点,一个极小值点,一个拐点B.有一个极大值点,一个极小值点,两个拐点C.有一个极大值点,一个极小值点,一个拐点D.有一个极大值点,两个极小值点,两个拐点
设函数y=f(x)的导函数,满足f′(一1)=0,当x<-l时,f′(x)<0;当x>-l时,f′(x)>0.则下列结论肯定正确的是( ).《》( )A.x=-1是驻点,但不是极值点B.x=-1不是驻点C.x=-1为极小值点D.x=-1为极大值点
设f(x)在(-a,a)是连续的偶函数,且当0A. f(0)是f(x)在(-a,a)的极大值,但不是最大值B. f(0)是f(x)在(-a,a)的最小值C. f(0)是f(x)在(-a,a)的极大值,也是最大值D. f(0)是曲线y=f(x)的拐点的纵坐标
设f(x)在(-a,a)是连续的偶函数,且当0()A、f(0)是f(x)在(-a,A.的极大值,但不是最大值B、B.f(0)是f(x)在(-a,的最小值C、C.f(0)足f(x)在(-a,的极大值,也是最大值D、f(0)是曲线y=f(x)的拐点的纵坐标
单选题设函数f(x)满足关系式f″(x)+[f′(x)]2=x,且f′(0)=0,则( )。Af(0)是f(x)的极大值Bf(0)是f(x)的极小值C点(0,f(0))是曲线y=f(x)的拐点Df(0)不是f(x)的极值,点(0,f(0))也不是曲线y=f(x)的拐点
单选题设f(x)在(-a,a)是连续的偶函数,且当0()Af(0)是f(x)在(-a,A.的极大值,但不是最大值BB.f(0)是f(x)在(-a,的最小值CC.f(0)足f(x)在(-a,的极大值,也是最大值Df(0)是曲线y=f(x)的拐点的纵坐标