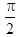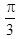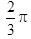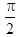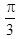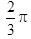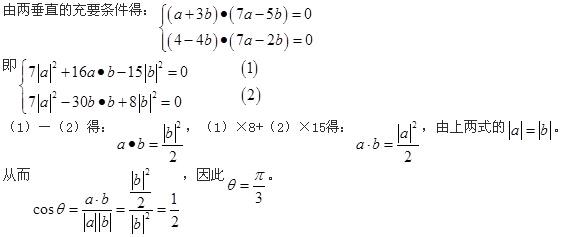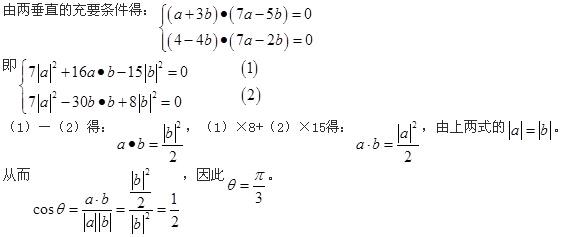已知向量a,b,c是三个具有公共起点的非零向量,且|a|=2|b|=2,又a·b=-1, 〈a-c,b-c 〉=π/3 ,则当|a-c|=7时,向量a与c的夹角是____.
设向量a=(-2,4,4),b=(0,6,3),则a与b的夹角为( ).A.B.C.D.
设α,β为四维非零列向量,且α⊥β,令A=αβ^T,则A的线性无关特征向量个数为().A.1B.2C.3D.4
设α,β,γ都是非零向量,若α×β=α×γ,则( )。A.β=γB.α//β且α//γC.α//(β-γ)D.α⊥(β-γ)
设向量α与向量β的夹角θ=π/3,模|α|=1,|β|=2,则模|α+β|等于( )
设a,b,c为非零向量,则与a不垂直的向量是( )。A.(a·c)b-(a·b)cB.C.a×bD.a+(a×b)×a
两个非零向量a和b,若∣a∣=∣b∣=∣a-b ∣,则a与a+b的夹角为_______.
设η为非零向量,A=,η为方程组AX=O的解,则a=_______,方程组的通解为_______.
设α,β为三维非零列向量,(α,β)=3,A=αβ^T,则A的特征值为_______.
设α1,α2,…,αn为n个线性无关的n维列向量,且与向量β正交.证明:向量β为零向量.
设a,b为非零向量,λ∈R+,满足|a+b|=λ|a-b|,则“λ>1”是“a,b的夹角为锐角”的( )A、充分不必要条件B、必要不充分条件C、充分必要条件D、既不充分也不必要条件
设a、b、c均为非零向量,则与a不垂直的向量是:()A、(a·C.b-(a·B.cB、B.b-(a·b/a·aC、a×bD、D.a+(a××a
设α,β,γ都是非零向量,若α×β=α×γ,则()。A、β=γB、α//β且α//γC、α//(β-γ)D、α⊥(β-γ)
设α,β,γ都是非零向量,α×β=α×γ,则()。A、β=γB、α∥β且α∥γC、α∥(β-γ)D、α⊥(β-γ)
单选题设a、b、c均为非零向量,则与a不垂直的向量是:()A(a·C.b-(a·B.cBB.b-(a·b/a·aCa×bDD.a+(a××a
单选题设α、β、γ都是非零向量,若α×β=α×γ,则( )。Aβ=γBα∥β且α∥γCα∥(β-γ)Dα⊥(β-γ)
单选题设a(→),b(→)为非零向量,且a(→)⊥b(→),则必有( )。A|a(→)+b(→)|=|a(→)|+|b(→)|B|a(→)+b(→)|=|a(→)|-|b(→)|C|a(→)+b(→)|=|a(→)-b(→)|Da(→)+b(→)=a(→)-b(→)
单选题设α,β,γ都是非零向量,α×β=α×γ,则()。Aβ=γBα∥β且α∥γCα∥(β-γ)Dα⊥(β-γ)