设a,b,c为非零向量,则与a不垂直的向量是( )。A.(a·c)b-(a·b)cB.C.a×bD.a+(a×b)×a
设a,b,c为非零向量,则与a不垂直的向量是( )。
A.(a·c)b-(a·b)c
B.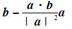
C.a×b
D.a+(a×b)×a
B.
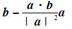
C.a×b
D.a+(a×b)×a
参考解析
解析:

相关考题:
下述结论中,不正确的有() A.若向量a与β正交,则对任意实数a,b,aα与bβ也正交B.若向量β与向量a1,a2都正交,则β与a1,a2的任一线性组合也正交C.若向量a与正交,则a,β中至少有一个是零向量D.若向量a与任意同维向量正交,则a是零向量.
设A,B为满足AB=0的任意两个非零矩阵,则必有(56)。A.A的列向量组线性相关,B的行向量组线性相关B.A的列向量组线性相关,B的列向量组线性相关C.A的行向量组线性相关,B的行向量组线性相关D.A的列向量组线性相关,B的列向量组线性相关
设A为m×n矩阵,则齐次线性方程组Ax=0有非零解的充分必要条件是( )。A、矩阵A的任意两个列向量线性相关B、矩阵A的任意两个列向量线性无关C、矩阵A的任一列向量是其余列向量的线性组合D、矩阵A必有一个列向量是其余列向量的线性组合
单选题设向量组Ⅰ:α(→)1,α(→)2,…,α(→)m,其秩为r;向量组Ⅱ:α(→)1,α(→)2,…, α(→)m,β(→),其秩为s,则r=s是向量组Ⅰ与向量组Ⅱ等价的( )。A充分非必要条件B必要非充分条件C充分必要条件D既非充分也非必要条件
单选题设向量组I:α(→)1,α(→)2,…,α(→)m,其秩为r;向量组II:α(→)1,α(→)2,…,α(→)m,β(→),其秩为s,则r=s是向量组I与向量组II等价的( )。A充分非必要条件B必要非充分条件C充分必要条件D既非充分也非必要条件
单选题设a(→),b(→)为非零向量,且a(→)⊥b(→),则必有( )。A|a(→)+b(→)|=|a(→)|+|b(→)|B|a(→)+b(→)|=|a(→)|-|b(→)|C|a(→)+b(→)|=|a(→)-b(→)|Da(→)+b(→)=a(→)-b(→)
单选题设α、β均为非零向量,则下面结论正确的是( )。[2017年真题]Aα×β=0是α与β垂直的充要条件Bα·β=0是α与β平行的充要条件Cα×β=0是α与β平行的充要条件D若α=λβ(λ是常数),则α·β=0