已知正六边形ABCDEF的边长为a,PA为过点A而垂直于正六边形所在平面M的垂线,且PA=a,求:(I)点P到AB、BC、CD各边的距离;(II)PD与平面M所成的角.
已知正六边形ABCDEF的边长为a,PA为过点A而垂直于正六边形所在平面M的垂线,且PA=a,求:
(I)点P到AB、BC、CD各边的距离;
(II)PD与平面M所成的角.
(I)点P到AB、BC、CD各边的距离;
(II)PD与平面M所成的角.

参考解析
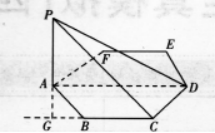
解析:(I)如图所示,
24题答案图
∵PA上平面M,∴PA上BC,
∴点P到AB的距离为a.过A作BC的垂线交CB的延长线于G,连结PG,
∴BC上平面APG,即PG⊥AB,

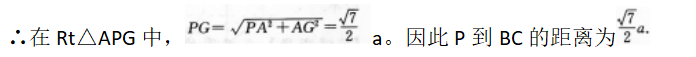
∵PA上平面M,
∴AC是PC在平面M上的射影,
又∵AD是正六边形ABCDEF外接圆的直径,
∴∠ACD=90o.
因此AC⊥CD,所以CD⊥平面ACP,即PC是P到CD的距离,
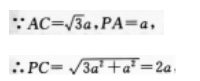
因此P到CD的距离为2a.
(Ⅱ)设PD与DA所夹的角为口,在Rt△PAD中,
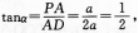
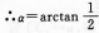 (VI)为PD与平面M所夹的角.
(VI)为PD与平面M所夹的角.

24题答案图
∵PA上平面M,∴PA上BC,
∴点P到AB的距离为a.过A作BC的垂线交CB的延长线于G,连结PG,
∴BC上平面APG,即PG⊥AB,

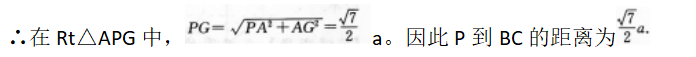
∵PA上平面M,
∴AC是PC在平面M上的射影,
又∵AD是正六边形ABCDEF外接圆的直径,
∴∠ACD=90o.
因此AC⊥CD,所以CD⊥平面ACP,即PC是P到CD的距离,
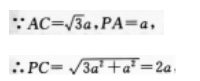
因此P到CD的距离为2a.
(Ⅱ)设PD与DA所夹的角为口,在Rt△PAD中,
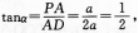
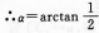 (VI)为PD与平面M所夹的角.
(VI)为PD与平面M所夹的角.
相关考题:
在半径为13的球面上有A , B, C 三点,AB=6,BC=8,CA=10,则(1)球心到平面ABC的距离为 ;(2)过A,B 在半径为13的球面上有A , B, C 三点,AB=6,BC=8,CA=10,则(1)球心到平面ABC的距离为 ;(2)过A,B两点的大圆面与平面ABC所成二面角(锐角)的正切值为 .
六边形ABCDEF中,AB∥ED,AF∥CD,BC∥FE,且AB=ED,AF=CD,BC=EF。又FD⊥BD,FD=24cm,BD=18cm,则六边形ABCDEF的面积为()。A.432cm2B.368cm2C.216cm2D.以上A、B、C均不正确
如图,在正点电荷Q的电场中有M、Ⅳ、P、F四点,M、N、P为直角三角形的三个顶点,F为MN的中点,<M=30。,M、N、P、F四点的电势分别用φm、φn、φpφf表示。已知φm=φn,φp=φf卢卿,点电荷Q在M、N、P三点所在的平面内,则( )。A.点电荷Q不一定在MP的连线上B.连接PF的线段一定在同一等势面上C.将正试探电荷从P点搬运到Ⅳ点,电场力做负功D.φp大于φm
已知37带内A点高斯平面坐标(XA,YA)和39带C点高斯平面坐标(XC,YC),下列说法正确的是()。A:A、B两点的平面距离为B:求两点间的距离需要高斯反算,得到大地坐标(BA,LA)、(BC,LC)C:求两点间的距离需要高斯正算,得到大地坐标(BA,LA)、(BC,LC)D:求两点的椭球面上的距离是计算两点的大地线E:求两点的椭球面上的距离是计算两点所在大圆的弦长
已知四棱锥P-ABCD底面为直角梯形,AB平行于DC,∠DAB=90°,PA垂直于底面ABCD,PA=AD=DC=AB=1,M为PB中点。 (1)求证:面PAD⊥面PCD; (2)求面AMC与面BMC所成二面角的余弦值。
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。 (1)证明:CD⊥平面PAE; (2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。
当试件截面积相同时,截面形状为圆形、方形和正六边形的试件,在相同试验条件下, 其试验测得的单轴抗压强度的大小关系最可能是()A、圆形方形正六边形B、圆形方形正六边形C、圆形正六边形方形D、方形圆形正六边形
设平面图形的加速度瞬心为M,则下列说法正确的是()A、图形上各点的加速度方向必与过该点与加速度瞬心M的直线垂直B、图形上各点的加速度大小必与该点到M的距离成正比C、图形上各点的加速度方向必与过该点及M点的直线间所夹的角都相等D、图形上各点的加速度分布与图形绕M点作定轴转动时相同
在测量平面直角坐标中,已知A点坐标(500.00m,500.00m),AB边坐标方位角αAB=210°00′00″,AB边水平距离DAB=100m,则B点坐标为:()A、(413.40m,450.00m)B、(450.00m,413.40m)C、(550.00m,413.40m)D、(586.60m,450.00m)
单选题在测量平面直角坐标中,已知A点坐标(500.00m,500.00m),AB边坐标方位角αAB=210°00′00″,AB边水平距离DAB=100m,则B点坐标为:()A(413.40m,450.00m)B(450.00m,413.40m)C(550.00m,413.40m)D(586.60m,450.00m)