假设企业1和企业2生产相同的产品且成本函数一样,其边际成本恒定且没有固定成本,即AC=MC-10,整个市场的需求函数为Q=200-p。请分别计算古诺模型和斯塔克伯格模型下的社会福利,并比较哪个大。
假设企业1和企业2生产相同的产品且成本函数一样,其边际成本恒定且没有固定成本,即AC=MC-10,整个市场的需求函数为Q=200-p。请分别计算古诺模型和斯塔克伯格模型下的社会福利,并比较哪个大。
参考解析
解析:由题意可得,企业的成本函数均为C=10q。(1)若两个企业之间进行古诺竞争,则两个企业的利润函数分别为:
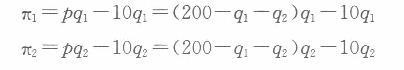
由利润最大化的一阶条件分别得:
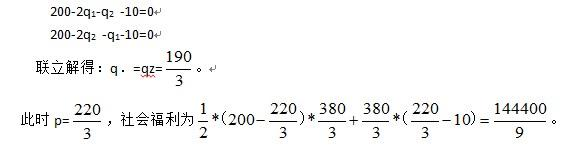
(2)若两个企业之间进行斯塔克伯格模型竞争,一家厂商为主导者时,假设厂商1为主导者,由(1)得厂商2的反应函数为
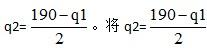
专]&代入企业l的利润函数得:
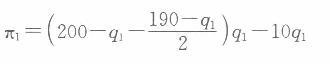
利润最大化的一阶条件为:

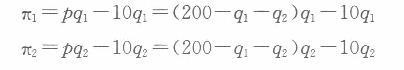
由利润最大化的一阶条件分别得:
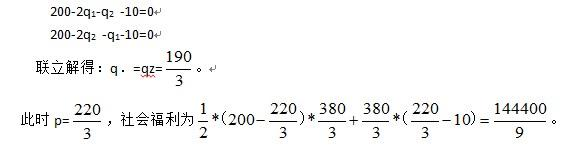
(2)若两个企业之间进行斯塔克伯格模型竞争,一家厂商为主导者时,假设厂商1为主导者,由(1)得厂商2的反应函数为
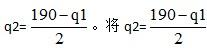
专]&代入企业l的利润函数得:
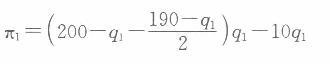
利润最大化的一阶条件为:

相关考题:
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果两个厂商同质,且在均衡价格上的需求弹性(以绝对值定义)为2,那么均衡时厂商的价格加成率是多少?
假设在一个市场上有两家企业,该市场的逆需求函数为P=4一罢,企业1的成本函数为 c1= q1,企业2的成本函数为C2 =2q2,P为价格,Q为两个企业的总产量,q为每个企业的产量。 (1)假设两个企业可以组成一个卡特尔,求垄断价格及每个企业的产量。 (2)试证明:卡特尔不是一个纳什均衡。 (3)假设两个企业进行产量竞争,求古诺均衡下的价格和每个企业的产量。
市场反需求函数为P=a-bQ,有N(N≥3)个同质企业,典型企业i的成本函数为TC(qi)=Qqi,其中Q为市场的总产量,且Q=(q1+q2…+qx)。 若各企业合并为一家,新的产量和利润为多少,并比较与第一问结果的区别。
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。假设企业处在长期生产中,w=1,v=4, 企业的最优生产方式是什么?企业的长期成本函数是什么?
市场上有两家企业E和D生产灯泡,市场需求函数Q=100-P。两家企业的成本函数Ci=10qi试求:(1)假设两方经理不认识,不共谋,都像短期完全竞争者那样行动,则该情形下的均衡价格和两厂商的均衡产量和利润各是多少?(2)假设两个企业换经理人了,要按照寡头垄断来,使用古诺模型,该情形下的均衡价格和两厂商均衡产量和利润各是多少?(3)E企业知道D企业准备按照古诺均衡来决定产量,现在E企业先按照斯塔克尔伯格模型来决定产量,则该情形下的均衡价格和两厂商的均衡产量和利润各是多少?(4)假设两方经理互相认识,两方共谋,则该情形下的均衡价格和两厂商的均衡产量和利润各是多少?
假设企业A和B生产同种商品,消费者无法区分两个企业的产品。企业A的生产边际成本为10,企业B的生产边际成本为8。他们的固定成本均为O。市场需求函数为: (1)如果企业A和企业B进行伯特兰竞争,那么纳什均衡条件下的市场价格是多少? (2)每个企业的利润分别为多少? (3)该均衡是否为帕累托有效?
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果两个厂商的生产均面临不变的边际成本1/2,且反需求曲线为p=1-Q,则均衡时两个企业的产量分别是多少?
某市场存在两家企业A和B,该市场的需求函数为P=100—ql一q2,其中q1和q2分别表示两家企业所销售的数量,如果这两家企业进行产量竞争,其边际成本都为20,并且没有固定的成本。(1)假设这两家企业同时选择产量,请计算两家企业各自的均衡产量。(2)若这两家企业合并为一家企业,请计算均衡产量。
微观经济学的问题,重谢!某垄断厂商的边际成本MC=40,该厂商面临的需求曲线Q=240-P.(1)求该垄断厂商均衡时的价格、产量和利润; (2)假设有第二个厂商加入该市场,且与第一个厂商有着相同的边际成本,求该市场的古诺模型解。
考虑以下古诺竞争模型。市场中有N个企业,生产相同的产品,均没有生产成本。市场需求函数为P=a-bQ,其中a,b>0,Q为行业总产量。如果企业同时展开产量竞争,那么: (1)均衡时价格是多少? (2)此时消费者剩余是多少?
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果均衡价格上的需求价格弹性仍为2,而均衡时行业的HHI指数(即每个企业占有总市场份额的平方和s12+s22)为0.68,以企业市场份额为权重计算的行业平均价格加成率为多少?(价格加成率以勒纳指数(p-MC)/p度量)
市场反需求函数为P=a-bQ,有N(N≥3)个同质企业,典型企业i的成本函数为TC(qi)=Qqi,其中Q为市场的总产量,且Q=(q1+q2…+qx)。 假设价格为P,求N个企业进行古诺竞争时每个企业的产量和利润,以及市场总产量和总利润。
假设有甲和乙两家企业,市场需求函数为Q=100-P,Q=q1+q2,两家企业的成本函数均为Ci=20qi,i=1,2。问:(1)试计算反应函数,古诺均衡的产量和利润。(2)如果企业甲不得不在企业乙选择q2的情况下选择q1,且甲明确知道企业乙的反应函数,问企业甲根据利润最大化决定的产量,利润是多少?企业乙的利润和产量是多少?(3)如果企业家可以在企业乙之前、同时或之后决定产量,请问企业甲该如何选择?
一个市场的需求函数为:P(Q)=100-2Q,企业的成本函数为:C(Q)=4Q,下列说法正确的有()。Ⅰ.若该市场为完全竞争市场,则均衡价格P=4,均衡产量为48Ⅱ.当市场上有2个企业时,若处于古诺均衡,则均衡价格是36Ⅲ.当市场上有2个企业时,若处于斯塔克尔伯格均衡,则均衡价格为36Ⅳ.当市场上有2个企业时,若达成卡特尔均衡,则两个企业都没有违约动机A.Ⅰ、ⅡB.Ⅰ、ⅢC.Ⅲ、ⅣD.Ⅰ、Ⅱ、Ⅳ
已知某完全垄断企业的需求函数为P=17-4Q,成本函数为TC=5Q+2Q2。 (1)计算企业利润最大化的价格和产出、利润。 (2)如果政府实行价格管制,按边际成本定价与按平均成本定价,价格分别是多少?厂商是否亏损?
多选题双寡头的古诺模型的基本假设是()A寡头市场只有两个企业B两个企业生产完全相同的产品C两个企业具有相同的成本函数D信息完全