某寡头行业有两个厂商,厂商l的成本函数为C1=8Q.,厂商2的成本函数为C2=0.8Q22,该市场的需求函数为P= 152 -0. 6Q.求:该寡头市场的古诺模型的解(保留一位小数).
某寡头行业有两个厂商,厂商l的成本函数为C1=8Q.,厂商2的成本函数为C2=0.8Q22,该市场的需求函数为P= 152 -0. 6Q.求:该寡头市场的古诺模型的解(保留一位小数).
参考解析
解析:由题意可知,在古诺模型的假设条件下,市场的线性需求函数为P= 152 -0.6(Q.+Q2)。
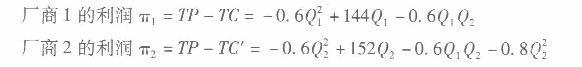

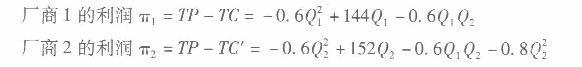

相关考题:
计算题:已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求: 计算题:已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场上价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数
计算题:已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求:(1)当市场商品价格为P=100时,厂商实现MR=LMC时的产量,平均成本和利润;(2)该行业长期均衡时的价格和单个厂商的产量;(3)当市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。
某成本不变的完全竞争行业的代表性厂商的长期总成本函数为LTC=Q3-60Q2+1500Q,产品价格P=975美元,市场需求函数为P=9600-2Q,试求:(1)利润极大时的产量、平均成本和利润。(2)该行业长期均衡时的价格和厂商的产量。(3)用图形表示上述(1)和(2)。(4)若市场需求曲线是P=9600-2Q,试问长期均衡中留存于该行业的厂商人数是多少?
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求:(1)当市场商品价格是P=100,厂商实现MR=LMC时的产量,平均成本和利润;(2)该行业长期均衡时的价格和单个厂商的产量;(3)市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。
假定某完全竞争行业有100个相同的厂商,单个厂商的短期总成本函数为.STC=Q2+6Q +20。 (l)求市场的短期供给函数。 (2)假定市场的需求函数为Qd=420 - 30P,求该市场的短期均衡价格和均衡产量。 (3)假定政府对每一单位商品征收1.6元的销售税,那么,该市场的短期均衡价格和均衡产量是多少?消费者和厂商各自负担多少税收?
某产品的市场需求曲线为Q=2O -P,市场中有n个生产成本相同的厂商,单个厂商的成本函数为c=2q2+2,问: (1)若该市场为竞争性市场,市场均衡时的市场价格和单个企业的产量是多少? (2)长期均衡时该市场中最多有多少个厂商? (3)若该市场为寡头垄断市场,古诺均衡时的市场价格和单个企业的产量是多少?
假定某寡头厂商面临一条弯折的需求曲线,产量在0~30单位范围内时需求函数为P=60-0.3Q,产量超过30单位时需求函数为P=66 -0.50;该厂商的短期总成本函数为STC=0.005 Q3-0. 2Q2 +36Q +200。 (1)求该寡头厂商利润最大化的均衡产量和均衡价格。 (2)假定该厂商成本增加,导致短期总成本函数变为STC =0.005Q3 -0.2Q2 +50Q +200,求该寡头厂商利润最大化的均衡产量和均衡价格。 (3)对以上(1)和(2)的结果作出解释。
完全竞争市场中厂商长期成本函数为c(q)= 1000 +1Oq2(g>o),q=0,c=O.市场需求函数为p =1200 - 2q。 (1)求厂商长期供给函数。 (2)长期均衡时行业中有多少厂商? (3)求长期均衡时的消费者剩余。
假定某寡头市场有两个厂商生产同种产品,市场的反需求函数为P=100—Q,两个厂商的成本函数分别为TC1=20Q,TC2=0.5Q22。 (1)假定两厂商按古诺模型行动,求两厂商各自的产量和利润量,以及行业的总利润量。 (2)假定两厂商联合行动组成卡特尔,追求共同利润最大化,求两厂商各自的产量和利润量,以及行业的总利润量。 (3)比较(1)与(2)的结果。
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数为LTC= Q3 - 12Q2+40Q。试求: (1)当市场产品价格为P=100时,厂商实现MR= LMC时的产量、平均成本和利润。 (2)该行业长期均衡时的价格和单个厂商的产量。 (3)当市场的需求函数为Q=660 -15P时,行业长期均衡时的厂商数量。
已知某完全竞争行业中的单个厂商的短期成本函数为STC =0.1Q3- 2Q2+150 +10 . (1)求当市场上产品的价格为P=55时,厂商的短期均衡产量和利润。 (2)当市场价格下降为多少时,厂商必须停产? (3)求厂商的短期供给函数。
假设某完全竞争行业有200个相同的企业,企业的短期成本函数为TC =0. 2Q2+Q+15,市场需求函数为Qp= 2475 - 95P,厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q,求: (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。
假设某完全竞争行业有500个相同的厂商,每个厂商的短期成本函数为:STC=O. 5Q2+Q+10。 (1)求完全竞争市场的短期供给函数。 (2)假设市场需求函数为QD=4 000-400P,求市场的均衡价格和产量。 (3)假定对每一件产品征收0.9元的税,新的市场均衡价格和产量又为多少?厂商和消费者的税收负担各为多少?
一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3(Q1+Q2),东部市场对该产品的需求函数为P1=15-Q1,西部市场对该产品的需求函数为P2=25一2Q2。 如果政府规定,禁止在不同市场上制定不同的价格,求此时该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。
某行业有两家寡头垄断厂商。厂商1的成本函数为c(y)=400+2y。该行业的市场需求曲线是一条向下倾斜的直线。在古诺均衡中( )。A.固定成本低的厂商生产的多B.固定成本高的厂商生产的多C.两家厂商生产的一样多D.条件不足,无法判断
在一个完全竞争的成本不变行业中,单个厂商的长期成本函数为LTC=Q3 - 40Q2+600Q,该市场的需求函数为Qd=13000 - 5P。求: (1)该行业的长期供给曲线。 (2)该行业实现长期均衡时的厂商数量。
一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3(Q1+Q2),东部市场对该产品的需求函数为P1=15-Q1,西部市场对该产品的需求函数为P2=25一2Q2。 如果该厂商可以将东西部市场区分开,在不同的市场制定不同的价格出售,求该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。
已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3—2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。
问答题已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求:(1)当市场商品价格是P=100,厂商实现MR=LMC时的产量,平均成本和利润;(2)该行业长期均衡时的价格和单个厂商的产量;(3)市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。
问答题已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3—2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。