假设一家企业的生产函数是f(K,L) = K2L2,其中L的价格是w,K的价格是r,请回答以下问题: (1)证明企业的生产技术是规模报酬递增的。 (2)长期扩展路径(long- run expansion path)是由资本和劳动最优组合所组成的曲线,请用画图的方法把这一路径找出来。 (3)如果w=10、r=2,请找出这条长期扩展路径具体的函数形式。
假设一家企业的生产函数是f(K,L) = K2L2,其中L的价格是w,K的价格是r,请回答以下问题: (1)证明企业的生产技术是规模报酬递增的。 (2)长期扩展路径(long- run expansion path)是由资本和劳动最优组合所组成的曲线,请用画图的方法把这一路径找出来。 (3)如果w=10、r=2,请找出这条长期扩展路径具体的函数形式。
参考解析
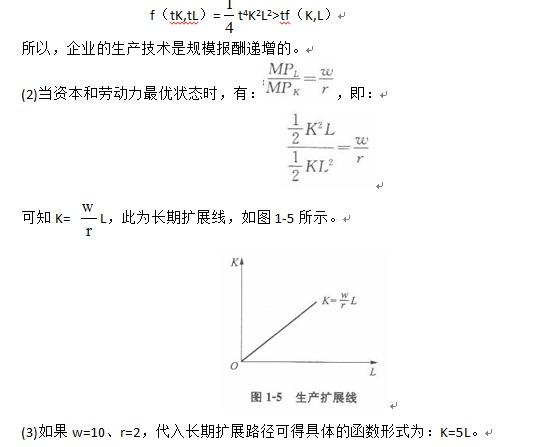
解析:(1)当L和K均扩大t倍(t>1)时,则有:

相关考题:
已知某企业的生产函数Q=L2/3K1/3 ,劳动的价格W=2,资本的价格r=1,求:(1)当成本C=3000时,企业实现最大产量时的L、K和Q的值。(2)当产量Q=800时,企业实现最少成本时的L、K和C的值。
竞争性市场上有N个厂商,他们具有相同的生产技术,生产相同的产品,所需的投入为资本K和能源L。其中,资本的单位价格为R;由于能源受政府管制,单位价格为W不变。生产函数f(K,L) =AKαL1-α。求各企业的供给曲线和行业总供给曲线。 求各企业的供给曲线和行业总供给曲线。
考虑一个罗宾逊孤岛模型。罗宾逊在岛上生产食品,生产函数为g=AL1/2,A>0,其中q为食品产量,L是劳动力投入使用量,A为外生参数。罗宾逊把每天24小时的时间在劳动(L)和休闲(R)之间进行分配。罗宾逊的效用函数是U=1nc+lnR,其中c为食品的消费数量。请解出该经济体最优的生产和消费。请问该资源分配方式可以通过完全竞争市场均衡实现吗?如果是,请求出市场均衡(包括均衡价格和均衡数量)。设食品的价格为p,劳动力价格为W。如果不是,请解释为什么。 下面考虑生产函数q=AL2
已知生产函数为Q =f(K,L)=KL -0. 5L2-0.32K2,Q表示产量,K表示资本,L表示劳动,若K =10,求: (1)写出劳动的平均产量和边际产量函数。 (2)计算当总产量达到极大值时企业雇佣的劳动人数。
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。假设企业处在长期生产中,w=1,v=4, 企业的最优生产方式是什么?企业的长期成本函数是什么?
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。假设该厂商产品的市场需求函数Q=a-0.5P。若劳动力市场是完全竞争的,求该厂商对劳动的需求函数。
假定一个竞争性厂商,其生产函数为Q=f(L,K)=AL^αK^β,生产要素L和K的价格分别为w和r。 (1)试求在K为不变投入时厂商的短期成本函数。 (2)求厂商的长期成本函数,并讨论不同的规模报酬对平均成本曲线形状的影响。
竞争性市场上有N个厂商,他们具有相同的生产技术,生产相同的产品,所需的投入为资本K和能源L。其中,资本的单位价格为R;由于能源受政府管制,单位价格为W不变。生产函数f(K,L) =AKαL1-α。若出现能源短缺,共有L可用于此行业投入,Li为第i个企业可买到的最多能源,求此时各企业的供给曲线和行业总供给曲线。
已知某企业的生产函数为Q=,L^(2/3)K^(1/3),劳动的价格,w=2,资本的价格r =1:求 (1)当成本C=3000时,企业实现最大产量时的L、K和Q的均衡值。 (2)当产量Q=800时,企业实现最小成本时的L、K和C的均衡值:
设生产函数为柯布道格拉斯函数Q=L^(1/3)K^(2/3),己知劳动力和资本的价格分别是w=1和r =2, (1)该生产函数代表了哪种类型的规模收益? (2)设企业的生产成本为3000,求两种要素的投入数量与总产量。 (3)设企业的生产产量为800,求两种要素的投入数量与企业所需付出的成本。
竞争性市场上有N个厂商,他们具有相同的生产技术,生产相同的产品,所需的投入为资本K和能源L。其中,资本的单位价格为R;由于能源受政府管制,单位价格为W不变。生产函数f(K,L) =AKαL1-α。若政府实行能源指标分配,每单位能源对应1单位能源指标,共L单位能源,N个企业参与能源指标的拍卖。求能源指标的价格。
考虑柯布一道格拉斯生产函数其中K袁示资本存量,L表示劳动量,要素价格分别是r和w。 (1)求短期成本函数STC(r,w,Y)(短期生产假定资本存量保持不变)。 (2)求长期成本函数LTC(r,w,Y)。 (3)讨论参数a、β的取值与规模报酬之间的关系。
假设一个厂商试图找出最适的劳工雇用量(L)和效率工资(W)来极大化它的利润,它的生产函数(F)是由劳工数量(L)和劳工的努力程度(effort)所组成的,e为每位劳工的努力程度,其中,劳工的努力程度又和工资呈正比,也就是如果厂商的利润函数为π=PXF[e(W)L]-WL,为简化问题,假设产品价格是固定的,且P-1。 (1)请分别对L和W求导,找出决定厂商利润极大化的均衡条件。 (2)如果给定劳工的努力程度和工资的关系,也就是请根据(1)找出的均衡条件,求出最适效率工资是多少?
考虑一个罗宾逊孤岛模型。罗宾逊在岛上生产食品,生产函数为g=AL1/2,A>0,其中q为食品产量,L是劳动力投入使用量,A为外生参数。罗宾逊把每天24小时的时间在劳动(L)和休闲(R)之间进行分配。罗宾逊的效用函数是U=1nc+lnR,其中c为食品的消费数量。 请写出新生产函数下该经济体最优的生产和消费。请问该资源分配方式可以通过完全竞争市场均衡实现吗?如果是,请求出市场均衡解。(包括均衡价格和均衡数量)。设食品的价格为p,劳动力的价格为w。如果不是,请解释为什么。
找出以下情况的总供给曲线: (1)生产函数为Q=3NK,劳动需求为Nd=10-2W/P,劳动供给为Ns=4W/P,经济的资本存量固定于K=4的水平。 (2)上题中所得到的总供给曲线所代表是哪种情况下的总供给曲线? (3)如果名义工资固定在3,那么(1)和(2)的答案会有什么变化?
对于生产函数Q=f(L,K)和成本方程C=wL+rK来说,在最优点生产要素组合点上应该有()A、等产量曲线和等成本线相切B、MRTSlk=w/rC、dk/dl=w/rD、MPl/MPk=w/r
已知某企业的生产函数为Q=50L^(3/5)K^(3/5)(Q为产量,L为劳动,K为资本),则()A、生产函数为规模报酬递增B、生产函数为规模报酬递减C、生产函数为规模报酬不变D、生产要素报酬递增E、生产要素报酬递减
问答题已知某厂商的生产函数为Q=0.5L1/3K2/3;当资本投入量K=50时资本的总价值为500;劳动的价格PL=5。求: (1)劳动的投入函数L=L(Q); (2)总成本函数、平均成本函数和边际成本函数; (3)当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少?
多选题假设短期成本为STC(Q)=w·L(Q)+r·K(_),其中,w和r分别为劳动和资本的价格,则下列关于各类成本的表达式正确的有( )。ATVC=w·L(Q)BAC=STC/Q=AFC+AVCCAVC=TVC/Q=w·L(Q)/QDMC=dSTC/dQ=w·dL/dQEAFC=TFC/Q=r·K(_)/Q
问答题已知企业的生产函数为Q=F(L,K)=LK-0.5L2-0.32K2,Q表示产量,K表示资本,L表示劳动,令K=10。试求劳动的平均产量函数(AP1)和边际产量函数(MP1)。