已知向量a=(3,4),向量b=(0,-2),则cos(a,b)的值为( )
已知向量a=(3,4),向量b=(0,-2),则cos(a,b)的值为( )
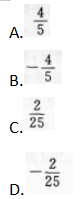
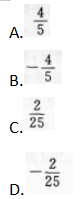
参考解析
解析:【考情点拨】本题主要考查e-j知识点为向量的夹角. 【应试指导】求cos〈a,b〉,可直接套用公式


相关考题:
设A为n阶实对称矩阵,则(). A.A的n个特征向量两两正交B.A的n个特征向量组成单位正交向量组C.A的k重特征值λ0,有r(λ0E-A)=n-kD.A的k重特征值λ。,有r(λ0E-A)=k
已知向量OA→=(-2,0),OB→=(2,2),BC→=(2cosθ,2sinθ)(0 ≤θ 已知向量OA→=(-2,0),OB→=(2,2),BC→=(2cosθ,2sinθ)(0 ≤θ(A)[7π/6 ,11π/6].(B)[7π/12 ,11π/12].(C)[2π/3 ,5π/3].(D)[5π/4 ,7π/4].
设直线的方程为则直线:(A)过点(1,-1,0),方向向量为2i + j-k(B)过点(1,-1,0),方向向量为2i - j + k(C)过点(-1,1,0),方向向量为-2i - j + k(D)过点(-1,1,0),方向向量为2i + j - k
已知向量a=(3cosα,3sinα),b=(2cosβ,2sinβ),若a与b的夹角为60°,则直线与圆(X-cosβ)2+(Y-sinβ)2=1的位置关系是( )。A.相交且不过圆心B.相交且过圆心C.相切D.相离
已知三维列向量a,β满足aTβ,设3阶矩阵A=βaT,则:A. β是A的属于特征值0的特征向量B. a是A的属于特征值0的特征向量C. β是A的属于特征值3的特征向量D. a是A的属于特征值3的特征向量
已知三维列向量αβ满足αTβ=3,设3阶矩阵A=βαT,则:A. β是A的属于特征值0的特征向量B. α是A的属于特征值0的特征向量C. β是A的属于特征值3的特征向量D. α是A的属于特征值3的特征向量
设A是三阶矩阵,a1(1,0,1)T,a2(1,1,0)T是A的属于特征值1的特征向量,a3(0,1,2)T是A的属于特征值-1的特征向量,则:A.a1-a2是A的属于特征值1的特征向量B.a1-a3是A的属于特征值1的特征向量C.a1-a3是A的属于特征值2的特征向量D. a1+a2+a3是A的属于特征值1的特征向量
A.过点(1,-1,0),方向向量为2i+j-kB.过点(1,-1,0),方向向量为2i-j+kC.过点(-1,1,0),方向向量为-2i-j+kD.过点(-1,1,0),方向向量为2i+j-k
设向量组α1=(1,0,1)T,α2=(0,1,1)T,a3=(1,3,5)T,不能由向量组β1,=(1,1,1)T,f12=(1,2,3)T,3β=(3,4,α)T线性表示。(1)求a的值;(2)将β1β2β2由α1α2α3线性表示。
已知λ= 2是三阶矩A的一个特征值,α1、α2是A的属于λ= 2的特征向量。 若α1=(1,2,0)T,α2=(1,0,1)T,向量β= (-1,2,-2)T,则Aβ等于( )。A. (2,2,1)T B. (-1,2,-2)T C. (-2,4,-4)T D. (-2,-4,4)
设直线的方程为,则直线()。A.过点(1,-1,0),方向向量为2i+j-kB.过点(1,-1,0),方向向量为2i-j+kC.过点(-1,1,0),方向向量为-2i-j+kD.过点(-1,1,0),方向向量为2i+j-k
已知λ=2是三阶矩阵A的一个特征值,α1,α2是A的属于λ=2的特征向量。若α1=(1,2,0)T,α2=(1,0,1)T,向量β=(-1,2,-2)T,则Aβ等于()。A、(2,2,1)TB、(-1,2,_2)TC、(-2,4,-4)TD、(-2,-4,4)
填空题已知空间向量,则2a+b=____.