微分方程(3+2y)xdx+(1+x2)dy=0 的通解为：A.1+x2=CyB. (1+x2)(3+2y)=CC.(3+2y)2=1/(1+x2)D. (1+x2)2(3+2y)=C
微分方程(3+2y)xdx+(1+x2)dy=0 的通解为：
A.1+x2=Cy
B. (1+x2)(3+2y)=C
C.(3+2y)2=1/(1+x2)
D. (1+x2)2(3+2y)=C
B. (1+x2)(3+2y)=C
C.(3+2y)2=1/(1+x2)
D. (1+x2)2(3+2y)=C
参考解析
解析：提示 判断方程的类型为可分离变量方程，将方程分离变量得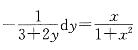
dx，两边积分计算。
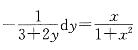dx，两边积分计算。
相关考题：
单选题设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（ ）。Ay″－y′＋y＝0By″－2y′＋2y＝0Cy″－2y′＝0Dy′＋2y＝0
填空题微分方程xy″＋3y′＝0的通解为____。