最新中考数学复习资料压轴题及答案
已知抛物线y=ax2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为_______。
2

已知过点(0,4),斜率为-1的直线l与抛物线C:y2—2px(b>;0)交于A,B两点.
(I)求C的顶点到2的距离;
(Ⅱ)若线段AB中点的横坐标为6,求C的焦点坐标.
分别写出抛物线y=4x2与y=-x2/4的开口方向、对称轴及顶点。
1.y=4x2
∵a=4>0 ∴开口向上
又∵b=c=0, ∴顶点在原点,对称轴为y轴
2. y=-x2/4
∵a=-1/4<0 ∴开口向下
又∵b=c=0, ∴顶点在原点,对称轴为y轴
先确定下列抛物线的开口方向、对称轴及顶点,再描点画图:
(1) y=-3x²+12x-3
(2) y=4x²-24x+26
(3)y=2x²+8x-6
(4)y=x²/2-2x-1
抛物线y=ax²+bx+c经过(-1,-22),(0,-8),(2,8)三点,求它的开口方向、对称轴和顶点坐标。
学习必备欢迎下载2011 中考数学复习资料 -压轴题及答案1.(20XX 年四川省宜宾市)已知 :如图 ,抛物线 y=-x2+bx+c 与 x 轴、 y 轴分别相交于点A(-1,0)、 B(0,3)两点,其顶点为 D. (1)求该抛物线的解析式;(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3)AOB 与 BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线y=ax2+bx+c(a0)的顶点坐标为abacab44,22). 2.(08 浙江衢州)已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,32),C(0,32),点 T在线段 OA 上(不与线段端点重合 ),将纸片折叠, 使点 A 落在射线 AB 上(记为点A),折痕经过点 T,折痕 TP 与射线 AB 交于点 P,设点 T 的横坐标为 t,折叠后纸片重叠部分 (图中的阴影部分 )的面积为 S;(1)求OAB 的度数,并求当点A在线段 AB 上时, S关于 t 的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t 的取值范围;(3)S 存在最大值吗?若存在,求出这个最大值,并求此时t 的值;若不存在,请说明理由 . 3. (08 浙江温州)如图,在RtABC中,90A,6AB,8AC,DE,分别是y x O B C A T y x O B C A T 学习必备欢迎下载边ABAC,的中点, 点P从点D出发沿DE方向运动, 过点P作PQBC于Q,过点Q作QRBA交AC于R,当点Q与点C重合时,点P停止运动设BQx,QRy(1)求点D到BC的距离DH的长;(2)求y关于x的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P,使PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由4.(08 山东省日照市)在ABC 中, A90 , AB4,AC3,M 是 AB 上的动点(不与A,B 重合),过M 点作 MNBC 交 AC 于点 N以 MN 为直径作 O,并在 O 内作内接矩形 AMPN令 AMx(1)用含 x 的代数式表示 NP 的面积 S;(2)当 x 为何值时,O 与直线 BC 相切?(3)在动点M 的运动过程中,记NP 与梯形 BCNM 重合的面积为y,试求 y 关于 x的函数表达式,并求x 为何值时, y 的值最大,最大值是多少?5、( 2007浙江金华)如图 1,已知双曲线y=xk(k0)与直线 y=k x交于 A,B两点,点A在第一象限. 试解答下列问题:(1) 若点 A的坐标为(4 , 2). 则点 B的坐标为;若点 A的横坐标为m ,则点 B的坐标可表示为;( 2)如图 2,过原点O作另一条直线l ,交双曲线y=xk(k0)于 P, Q两点,点P在第一象限 . 说明四边形APBQ 一定是平行四边形;设点A.P 的横坐标分别为m , n,A B C M N P 图3 O A B C M N D 图2 O A B C M N P 图1 O A B C D E R P H Q 学习必备欢迎下载四边形APBQ 可能是矩形吗?可能是正方形吗?若可能, 直接写出mn应满足的条件;若不可能,请说明理由. 6.(2008浙江金华)如图 1,在平面直角坐标系中,己知 AOB 是等边三角形,点A的坐标是(0 , 4) ,点 B在第一象限,点P是 x轴上的一个动点,连结AP,并把 AOP绕着点 A按逆时针方向旋转. 使边 AO与 AB重合 . 得到 ABD.( 1)求直线AB的解析式;( 2)当点 P运动到点(3,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使 OPD 的面积等于43,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由. 7.(2008 浙江义乌 )如图 1,四边形ABCD 是正方形, G 是 CD 边上的一个动点(点 G 与 C、D不重合 ),以 CG 为一边在正方形ABCD 外作正方形CEFG,连结 BG,DE我们探究下列图中线段 BG、线段 DE 的长度关系及所在直线的位置关系:(1)猜想如图1 中线段 BG、线段 DE 的长度关系及所在直线的位置关系;将图 1 中的正方形CEFG 绕着点C 按顺时针 (或逆时针 )方向旋转任意角度,得到如图2、如图 3 情形请你通过观察、测量等方法判断中得到的结论是否仍然成立 ,并选取图2 证明你的判断B A O P Q 图 2 x y B A O 图 1 学习必备欢迎下载( 2)将原题中正方形改为矩形(如图 46),且 AB=a,BC=b,CE=ka,CG=kb (ab,k0),第(1)题中得到的结论哪些成立,哪些不成立?若成立,以图 5 为例简要说明理由( 3)在第 (2)题图 5 中,连结DG、BE,且 a=3,b=2,k=12,求22BEDG 的值8. (2008 浙江义乌 )如图 1 所示,直角梯形OABC 的顶点 A、C 分别在 y 轴正半轴与x轴负半轴上 . 过点 B、C 作直线l将直线l平移,平移后的直线l与x轴交于点D ,与y轴交于点E( 1)将直线l向右平移, 设平移距离CD 为t(t0),直角梯形 OABC 被直线l扫过的面积(图中阴影部份)为s,s关于t的函数图象如图2 所示,OM 为线段, MN 为抛物线的一部分, NQ 为射线, N 点横坐标为4求梯形上底AB 的长及直角梯形OABC 的面积;当42t时,求 S关于t的函数解析式;( 2)在第( 1)题的条件下,当直线l向左或向右平移时(包括l与直线BC 重合),在直线AB 上是否存在点P,使PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P 的坐标 ;若不存在,请说明理由9.(2008 山东烟台 )如图,菱形ABCD 的边长为 2,BD=2 ,E、F 分别是边 AD ,CD 上的两个动点,且满足AE+CF=2. (1)求证: BDE BCF ;(2)判断 BEF 的形状,并说明理由;(3)设 BEF 的面积为S,求 S 的取值范围 . 学习必备欢迎下载10.(2008 山东烟台 )如图, 抛物线21:23Lyxx交x轴于 A、B 两点, 交y轴于 M 点.抛物线1L向右平移2 个单位后得到抛物线2L,2L交x轴于 C、D 两点 . (1)求抛物线2L对应的函数表达式;(2)抛物线1L或2L在x轴上方的部分是否存在点N,使以 A,C,M, N 为顶点的四边形是平行四边形 .若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点 P 是抛物线1L上的一个动点(P不与点 A、B 重合),那么点P 关于原点的对称点 Q 是否在抛物线2L上,请说明理由. 11.2008 淅江宁波 )20XX 年 5 月 1 日,目前世界上最长的跨海大桥杭州湾跨海大桥通车了通车后,苏南A 地到宁波港的路程比原来缩短了120 千米已知运输车速度不变时,行驶时间将从原来的3 时 20 分缩短到 2 时(1)求 A 地经杭州湾跨海大桥到宁波港的路程(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A 地到宁波港的运输成本是每千米1.8 元,时间成本是每时28 元,那么该车货物从A 地经杭州湾跨海大桥到宁波港学习必备欢迎下载的运输费用是多少元?(3)A 地准备开辟宁波方向的外运路线,即货物从A 地经杭州湾跨海大桥到宁波港,再从宁波港运到B 地若有一批货物 (不超过10 车)从 A 地按外运路线运到B 地的运费需8320元,其中从A 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10 车的货物计费方式是:一车800 元,当货物每增加1 车时,每车的海上运费就减少20 元,问这批货物有几车?12.(2008 淅江宁波 )如图 1,把一张标准纸一次又一次对开,得到“2开”纸、“ 4 开”纸、“ 8 开”纸、“ 16 开”纸已知标准纸的短边长为a(1)如图 2,把这张标准纸对开得到的“16 开”张纸按如下步骤折叠:第一步将矩形的短边AB与长边AD对齐折叠,点B落在AD上的点B处,铺平后得折痕AE;第二步将长边AD与折痕AE对齐折叠,点D正好与点E重合,铺平后得折痕AF则:AD AB的值是,ADAB,的长分别是,(2)“ 2 开”纸、“ 4 开”纸、“ 8 开”纸的长与宽之比是否都相等?若相等,直接写出这个比值;若不相等,请分别计算它们的比值(3)如图 3,由 8 个大小相等的小正方形构成“L”型图案, 它的四个顶点EFGH, , ,分别在“ 16 开”纸的边ABBCCDDA,上,求DG的长(4)已知梯形MNPQ中,MNPQ,90M,2MNMQPQ,且四个顶点MNPQ, ,都在“ 4开”纸的边上,请直接写出2 个符合条件且大小不同的直角梯形的面积13.(2008 山东威海)如图,在梯形ABCD 中, ABCD,AB7,CD1, ADBC5点M,N 分别在边AD,BC 上运动,并保持MNAB,MEAB,NFAB,垂足分别为E,F(1)求梯形ABCD 的面积;(2)求四边形MEFN 面积的最大值(3)试判断四边形MEFN 能否为正方形,若能,求出正方形MEFN 的面积;若不能,请说明理由A B C D B C A D E G H F F E B4开2 开8 开16开图 1 图 2 图 3 a 标准纸“ 2 开”纸、“ 4开”纸、“ 8 开”纸、“ 16开”纸都是矩形本题中所求边长或面积都用含a的代数式表示学习必备欢迎下载14( 2008 山东威海)如图,点A(m, m 1),B(m3,m1)都在反比例函数xky的图象上(1)求 m,k 的值;(2)如果 M 为 x 轴上一点, N 为 y轴上一点,以点 A,B, M,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式(3)选做题 :在平面直角坐标系中,点P 的坐标为( 5,0),点 Q 的坐标为( 0,3),把线段PQ 向右平移 4 个单位,然后再向上平移2个单位,得到线段P1Q1,则点 P1的坐标为,点 Q1的坐标为C D A B E F N M x O y A B 友情提示 :本大题第( 1)小题4 分,第( 2)小题7分对完成第( 2)小题有困难的同学可以做下面的(3)x O y 1 2 3 1 Q P 2 P1 Q1 学习必备欢迎下载A O B M D C 图 12 y x 15( 2008 湖南益阳) 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线. 如图 12,点 A、B、C、D 分别是“蛋圆”与坐标轴的交点,已知点D 的坐标为 (0 ,-3) ,AB 为半圆的直径,半圆圆心M 的坐标为 (1,0),半圆半径为2. 、(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;(2) 你能求出经过点C 的“蛋圆”切线的解析式吗?试试看;(3)开动脑筋想一想,相信你能求出经过点D 的“蛋圆”切线的解析式.学习必备欢迎下载16.(20XX 年浙江省绍兴市)将一矩形纸片OABC放在平面直角坐标系中,(0 0)O,(6 0)A,(0 3)C,动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动23秒时,动点P从点A出发以相等的速度沿AO向终点O运动当其中一点到达终点时,另一点也停止运动设点P的运动时间为t(秒)(1)用含t的代数式表示OPOQ,;(2)当1t时,如图 1,将OP Q沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;(4)连结AC,将OPQ沿PQ翻折,得到EPQ,如图 2问:PQ与AC能否平行?PE与AC能否垂直?若能,求出相应的t值;若不能,说明理由图 1 O P A x B D C Q y 图 2 O P A x B C Q y E 学习必备欢迎下载17.(20XX 年辽宁省十二市)如图 16,在平面直角坐标系中,直线33yx与x轴交于点A,与y轴交于点C,抛物线2
抛物线 y=ax²+bx+c与x轴的公共点是(-1 , 0),(3 , 0),求这条抛物线的对称轴。
先确定下列抛物线的开口方向、对称轴及顶点坐标,再描点画图:
(1) y=x²+2x-3
(2)y=1+6x-x2
(3)y=x2/2+2x+1
(4)y=-x2/4+x-4
(2)抛物线y=ax²+bx+c与x轴的两交点的横坐标分别是-1/2,3/2,与y轴交点的纵坐标是-5。
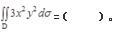
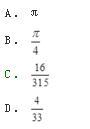

计算得抛物线与x轴、y轴的交点分别为(1,0)、(0,1),从而D={(x,y)|0≤y≤1-x2,x∈[0,1]},则
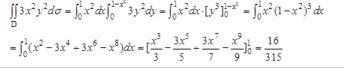
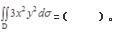
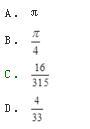
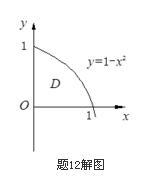
计算得抛物线与x轴、y轴的交点分别为(1,0)、(0,1),从而D={(x,y)|0≤y≤1-x2,x∈[0,1]},则
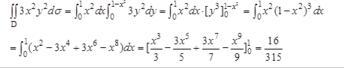
相关考题:
- 多选题下列物权中,属于用益物权的有()。A土地承包经营权B建设用地使用权C抵押权D地役权
- 在冻土密度试验中,对于温度高于-3℃的粘质和砂质冻土采用()。A、浮称法B、联合测定法C、环刀法D、充砂法
- 混凝土预制构件结构性能检测取样数量:在每批中随机抽取三块多孔板作为试件进行检验。
- 名词解释题附新股认购权公司债
- 多选题女性,78岁,腰背疼痛3年。加重10天,伴乏力,有时全身疼痛,晚间亦疼痛,轻度影响睡眠。10天前,按摩后腰背疼痛加重,严重影响睡眠。查体:老年女性。“驼背”,胸腰椎多处叩击痛(+),椎旁压痛(±),双上下肢无异常,X线示T12陈旧性压缩骨折。既往高血压病史20年,否认糖尿病病史。该患者出现此类临床表现,其病因可以包括()。A骨肿瘤或骨转移瘤致椎体破坏,出现压缩性骨折B绝经后,雌激素缺乏,骨丢失加速C成骨细胞功能与活性缺陷致骨形成不足和骨丢失D老龄和肾功能减退致肠钙吸收和VitD3生成减少E遗传因素,骨质量下降F合并甲亢、甲旁亢、库欣综合征等内分泌代谢疾病
- 单选题个人定期一本通、借记卡内个人定期存款单笔存入最高限额为人民币()万元(含)。A500B1000C2000D5000
- 多选题患者女性,25岁。以“阵发性双手手指指端苍白和发绀2年”入院。患者2年前因受寒出现双手手指指端苍白,继而发紫,逐渐扩展至整个手指,伴有针刺感,发作可持续一个小时以上,寒冷刺激解除后,15~30分钟左右皮色恢复正常。有时候情绪激动也会诱发。临床上常用的治疗该疾病的药物包括()。A硝苯地平B妥拉唑啉C多巴胺D利舍平E甲基多巴F硝酸甘油软膏
- 单选题已认定为小企业的客户,由于生产经营扩大连续两年超过小企业认定标准上限的,经一级分行批准后,在第()年初方可调出小企业客户范围。A2B3C4D5
- 单选题下列财产可以抵押的是()A土地所有权;B学校、幼儿园的教育设施;C依法被查封、扣押、监管的财产;D以招标、拍卖、公开协商等方式取得的荒地等土地承包经营权;
- 在《土工试验方法标准》(GB/T50123-1999)中,室温是()时,不可以进行收缩试验。A、25℃B、30℃C、35℃D、40℃