函数y=cosx在[0,2x]上满足罗尔定理,则ξ= .
函数y=cosx在[0,2x]上满足罗尔定理,则ξ= .
参考解析
解析:【答案】π【考情点拨】本题考查了罗尔定理的知识点.
【应试指导】
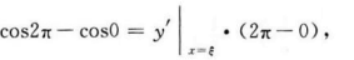

【应试指导】
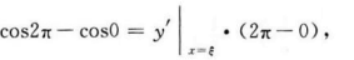

相关考题:
罗尔定理:设函数(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)(a)=(b),则在(a,b)内至少存在一点ξ,使得,′(ξ)=0。证明这个定理并说明其几何意义。
方程y"=sinx+cosx的通解为()。A、y=sinx+cosx+C1x+C2B、y=-sinx-cosx+C1x+C2C、y=sinx-cosx+C1x+C2D、y=-sinx+cosx+C1x+2
单选题已知曲线y=y(x)经过原点,且在原点的切线平行于直线2x-y-5=0,而y(x)满足y″-6y′+9y=e3x,则y(x)等于( )。Asin2xBx2e2x/2+sin2xCx(x+4)e3x/2D(x2cosx+sin2x)e3x
单选题曲线y-=cosx在[0,2π]上与x轴所围成图形的面积是:()A0B4C2D1