设X,Y相互独立且都服从(0,2)上的均匀分布,令Z=min{X,Y},则P(0
设X,Y相互独立且都服从(0,2)上的均匀分布,令Z=min{X,Y},则P(0
参考解析
解析:由X,Y在(0,2)上服从均匀分布得 
因为x,Y相互独立,所以
Fz(z)=P(Z≤z)=1-P(Z>z)=1-P(min{X,Y)}>z)=1-P(X>z,Y>z)
=1-P(X>z)P(Y>z)=1=【1-P(X≤z)】【1-P(Y≤z)】
=1-【1-Fx(z)】【1-FY(z)】,
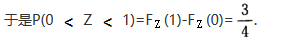

因为x,Y相互独立,所以
Fz(z)=P(Z≤z)=1-P(Z>z)=1-P(min{X,Y)}>z)=1-P(X>z,Y>z)
=1-P(X>z)P(Y>z)=1=【1-P(X≤z)】【1-P(Y≤z)】
=1-【1-Fx(z)】【1-FY(z)】,
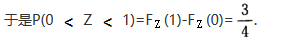
相关考题:
设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y的概率分布为P{Y=0}=P{Y=1}=.记Fz(z)为随机变量Z=XY的分布函数,则函数Fz(z)的间断点个数为 A.A0B.1C.2D.3
设随机变量X与Y相互独立,X服从参数为1的指数分布,Y的概率分布为P{Y=-1}=p,P{Y=1)=1-p,(0 (Ⅰ)求Z的概率密度; (Ⅱ)p为何值时,X与Z不相关; (Ⅲ)X与Z是否相互独立?
单选题设随机变量X与Y相互独立,且X在区间[0,2]上服从均匀分布,Y服从参数为3的指数分布,则数学期望E(XY)等于()。A1B3