设随机变量X,Y相互独立,X~U(0,2),Y~E(1),则.P(X+Y>1)等于().
设随机变量X,Y相互独立,X~U(0,2),Y~E(1),则.P(X+Y>1)等于().


参考解析
解析: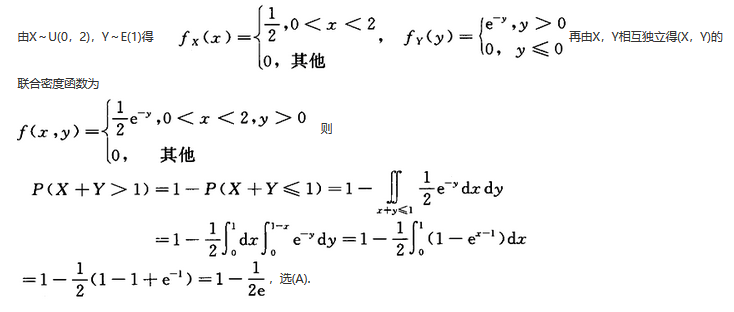
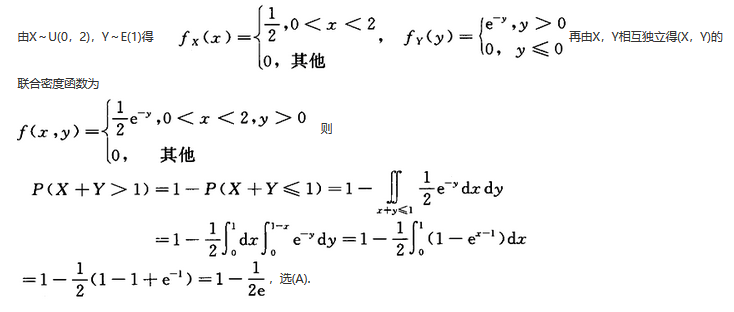
相关考题:
设随机变量X~N(1,2),Y~N(-1,2),Z~N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2+bZ2~χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3. 设随机变量U=max{X,Y},V=min{X,Y}. (1)求二维随机变量(U,V)的联合分布;(2)求Z=UV的分布; (3)判断U,V是否相互独立?(4)求P(U=V).
设两个随机变量X与Y相互独立且同分布,P{X=-1}=P{Y=-1}=1/2,P{X=1}=P{Y=1}=1/2,则下列各式成立的是()A、P{X=Y}=1/2B、P{X=Y}=1C、P{X+Y=0}=1/4D、P{XY=1}=1/4
单选题设两个随机变量X与Y独立同分布,P{X=-1}=P{Y=-1}=1/2,P{X=1}=P{Y=1}=1/2,则下列式子中成立的是( )。AP{X=Y}=1/2BP{X=Y}=1CP{X+Y=0}=1/4DP{XY=1}=1/4
单选题设随机变量X与Y相互独立,已知P(X≤1)=p,P(Y≤1)=q,则P(max(X,Y)≤1)等于().Ap+qBpqCpDq