已知f(x)是二阶可导的函数,y=e2f(x),A. e2f(x) B. e2f(x)f''(x)C. e2f(x)[2f'(x)] D.2e2f(x) {2[f'(x)]2+f''(x)}
已知f(x)是二阶可导的函数,y=e2f(x),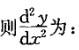
A. e2f(x) B. e2f(x)f''(x)
C. e2f(x)[2f'(x)] D.2e2f(x) {2[f'(x)]2+f''(x)}
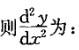
A. e2f(x) B. e2f(x)f''(x)
C. e2f(x)[2f'(x)] D.2e2f(x) {2[f'(x)]2+f''(x)}
参考解析
解析:提示:计算抽象函数的复合函数的二次导数:
S' =e2f(x) ? 2f'(x) = 2f'(x)e2f(x)
S''=2[f''(x)e2f(x)) + f'(x)? e2f(x)? 2f'(x)]
=2e2f(x) {2[f'(x)]2+f''(x)}
S' =e2f(x) ? 2f'(x) = 2f'(x)e2f(x)
S''=2[f''(x)e2f(x)) + f'(x)? e2f(x)? 2f'(x)]
=2e2f(x) {2[f'(x)]2+f''(x)}
相关考题:
设y=f(x)是(a,b)内的可导函数,x和x+Δx是(a,b)内的任意两点,则:A. Δy=f' (x)ΔxB.在x,x+Δx之间恰好有一点ξ,使Δy=f' (ξ)ΔxC.在x,x+Δx之间至少有一点ξ,使Δy=f' (ξ)ΔxD.在x,x+Δx之间任意一点ξ,使Δy=f' (ξ)Δx
设f(x),f'(x)为已知的连续函数,则微分方程y'十f'(x)y=f(x)f'(x)的通解是:A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +cC. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)
设y=f(x)是(a, b)内的可导函数,X,X+ΔX是(a, b)内的任意两点,则:(A) Δy= f‘ (x)Ax(B)在x,x+Ax之间恰好有一点ξ,使Δy=f'(ξ)Ax(C)在x, x+Ax之间至少有一点ξ,使Δy=f'(ξ)Ax(D)对于x,x+ax之间任意一点ξ,使Δy=f'(ξ)Ax
设y=f(x)是(a,b)内的可导函数,x,x+△x是(a,b)内的任意两点,则:A. △y=f’(x)△xB.在x,x+△x之间恰好有一点ξ,使△y=f’(ξ)△xC.在x,x+△x之间至少存在一点ξ,使△y=f’(ξ)△xD.在x,x+△x之间的任意一点ξ,使△y=f’(ξ)△x
已知f(x)是二阶可导的函数,y=e2f(x),则dy2/dx2为:A. e2f(x)B. e2f(x)f''(x)C. e2f(x)[2f'(x)]D.2e2f(x) {2[f'(x)]2+f''(x)}
函数y=f(x)在(a,6)内二阶可导,且f′(x)>0,f″(x)<0,则曲线y=f(x)在(a,6)内( ).《》( )A.单调增加且为凹B.单调增加且为凸C.单调减少且为凹D.单调减少且为凸
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af″(x)+f(x)=0Bf′(x)+f(x)=0Cf″(x)+f′(x)=0Df″(x)+f′(x)+f(x)=0
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A1/5B1/7C-1/7D-1/5
单选题(2009)设y=f(x)是(a,b)内的可导函数,x+△x是(a,b)内的任意两点,则:()A△y=f′(x)△xB在x,x+△x之间恰好有一点ξ,使△y=f′(ξ)△xC在x,x+△x之间至少有一点ξ,使△y=f′(ξ)△xD在x,x+△x之间任意一点ξ,使△y=f′(ξ)△x
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A1B-1C1/7D-1/7
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af′(x)+f(x)=0Bf′(x)-f(x)=0Cf″(x)+f(x)=0Df″(x)-f(x)=0