设y=f（x）是（a，b）内的可导函数，x，x+△x是（a，b）内的任意两点，则：A. △y=f’（x）△xB.在x，x+△x之间恰好有一点ξ，使△y=f’（ξ）△xC.在x，x+△x之间至少存在一点ξ，使△y=f’（ξ）△xD.在x，x+△x之间的任意一点ξ，使△y=f’（ξ）△x

设y=f（x）是（a，b）内的可导函数，x，x+△x是（a，b）内的任意两点，则：

A. △y=f’（x）△x
B.在x，x+△x之间恰好有一点ξ，使△y=f’（ξ）△x
C.在x，x+△x之间至少存在一点ξ，使△y=f’（ξ）△x
D.在x，x+△x之间的任意一点ξ，使△y=f’（ξ）△x

参考解析

解析：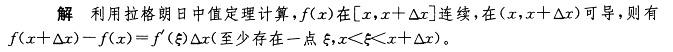

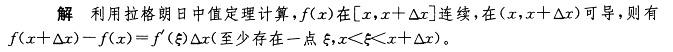
相关考题：

设X、Y的联合分布函数是F(x,y),则F(＋∞,y)等于:() A、0;B、1;C、Y的分布函数;D、Y的密度函数。
查看答案
设函数y=f(x)在(0，+∞)内有界且可导，则( )。A.B.C.D.
查看答案
设f（x）、f'（x）为已知的连续函数，则微分方程y'+ f'（x）y = f（x）f'（x）的通解是：
查看答案
设y=f(x)是(a,b)内的可导函数，x和x+Δx是(a,b)内的任意两点，则:A. Δy=f' (x)ΔxB.在x，x+Δx之间恰好有一点ξ，使Δy=f' (ξ)ΔxC.在x，x+Δx之间至少有一点ξ，使Δy=f' (ξ)ΔxD.在x，x+Δx之间任意一点ξ，使Δy=f' (ξ)Δx
查看答案
设y=f(x)是(a, b)内的可导函数，X,X+ΔX是(a, b)内的任意两点，则：(A) Δy= f‘ (x)Ax(B)在x，x+Ax之间恰好有一点ξ，使Δy=f'(ξ)Ax(C)在x, x+Ax之间至少有一点ξ，使Δy=f'(ξ)Ax(D)对于x，x+ax之间任意一点ξ，使Δy=f'(ξ)Ax
查看答案
设函数f(x)在(-∞，+∞)内连续，其二阶导函数f"(x)的图形如图所示，则曲线y=f(x)的拐点个数为　　 A.A0B.1C.2D.3
查看答案
设函数，(u)可导，z=f(sin y-sin x)+xy，则=__________.
查看答案
设f(x)是周期为4的可导奇函数，且f'(x)=2(x-1)，x∈［0，2］，则f(7)=________.
查看答案
下列命题中，正确的是( ).A.单调函数的导函数必定为单调函数B.设f(x)为单调函数，则f(x)也为单调函数C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点D.设f(x)在(a，b)内可导且只有一个极值点xo，f(xo)=0
查看答案
设f（x）和g（x）在（-∞，+∞）内可导，且f（x）＜g（x），则必有（ ）《》（ ）
查看答案
填空题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。
查看答案
填空题设函数f（x）在x＝2的某邻域内可导，且f′（x）＝ef（x），f（2）＝1，则f‴（2）＝____。
查看答案
单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A1/5B1/7C－1/7D－1/5
查看答案
填空题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。
查看答案
单选题（2009）设y=f（x）是（a，b）内的可导函数，x+△x是（a，b）内的任意两点，则：（）A△y=f′（x）△xB在x，x+△x之间恰好有一点ξ，使△y=f′（ξ）△xC在x，x+△x之间至少有一点ξ，使△y=f′（ξ）△xD在x，x+△x之间任意一点ξ，使△y=f′（ξ）△x
查看答案
单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A1B－1C1/7D－1/7
查看答案
单选题若函数f（x）在区间（a，b）内可导，x1和x2是区间（a，b）内任意两点（x1＜x2），则至少存在一点ξ，使（　　）Af（b）－f（a）＝f′（ξ）（b－a）（a＜ξ＜b）Bf（b）－f（x1）＝f′（ξ）（b－x1）（x1＜ξ＜b）Cf（x2）－f（x1）＝f′（ξ）（x2－x1）（x1＜ξ＜x2）Df（x2）－f（a）＝f′（ξ）（x2－a）（a＜ξ＜x2）
查看答案
单选题设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝（　　）。A1B2C3D4
查看答案
填空题设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝____。
查看答案
问答题设f（x）在（a，b）内二阶可导，且f″（x）≥0，证明：对于（a，b）内任意两点x1、x2及0≤t≤1，有f[（1－t）x1＋tx2]≤（1－t）f（x1）＋tf（x2）。
查看答案
填空题设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。
查看答案
单选题设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。A对任意x，f′（x）＞0B对任意x，f′（x）≤0C函数－f（－x）单调增加D函数f（－x）单调增加
查看答案
填空题设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝____。
查看答案
单选题设函数f（x）在x＝2的某邻域内可导，且f′（x）＝ef（x），f（2）＝1，则f‴（2）＝（　　）。Ae2B2e2Ce3D2e3
查看答案
单选题设函数f（x）在区间[1，＋∞）内二阶可导，且满足条件f（1）＝f′（1）＝0，x＞1时f″（x）＜0，则g（x）＝f（x）/x在（1，＋∞）内（　　）。A曲线是向上凹的B曲线是向上凸的C单调减少D单调增加
查看答案
单选题设函数f（u）可导，y＝f（x2），当自变量x在x＝－1处取得增量Δx＝－0.1时，相应的函数的增量Δy的线性主部为0.1，则f′（1）＝（　　）。A－1B0.1C1D0.5
查看答案
热门标签