n足够大.p不接近于0或1,样本率与总体率比较,统计量μ为A.B.C.D.|p-π|σE.
n足够大.p不接近于0或1,样本率与总体率比较,统计量μ为
A.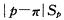
B.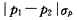
C.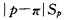
D.|p-π|σ
E.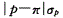
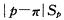
B.
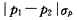
C.
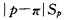
D.|p-π|σ
E.
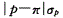
参考解析
解析:在样本含量n足够大、样本率p和1-p均不接近于零的前提下,样本率的分布近似于正态分布,样本率和总体率之间、两个样本率之间差异来源的判断可用μ检验。样本率与总体率的比较公式为: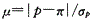 。故选E。
。故选E。
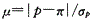 。故选E。
。故选E。
相关考题:
(2003)n足够大,P不接近于0或1,样本率与总体率比较,统计量u为A.|P-π|/SpB.|P-P|/σSXB (2003)n足够大,P不接近于0或1,样本率与总体率比较,统计量u为A.|P-π|/SpB.|P-P|/σC.|P-P|/SD.|P-π|/σE.|P-π|/σ
对于二项分布的资料符合下面哪种情况时,可借用正态分布处理()。A、样本含量n足够大,以致np(p为样本率)与n(1-p)都较大时B、样本含量n足够大,样本率p足够小时C、样本率p=0.5时D、样本率p接近1或0时E、样本率p足够大时
当样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为()A、P±2.58SpB、P±1.96SpC、P±1.96SxD、P±2.58SxE、X±1.96Sx
当样本含量足够大时,样本率又不接近0或1时,以样本率推断总体率95%可信区间的计算公式为()A、p±2.58sPB、p+1.645sPC、p±1.96sPD、π±1.96σπE、X±1.96sX
单选题对于二项分布的资料符合下面哪种情况时,可借用正态分布处理()。A样本含量n足够大,以致np(p为样本率)与n(1-p)都较大时B样本含量n足够大,样本率p足够小时C样本率p=0.5时D样本率p接近1或0时E样本率p足够大时
单选题当样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为()AP±2.58SpBP±1.96SpCP±1.96SxDP±2.58SxEX±1.96Sx