下列矩阵中不能相似对角化的为( )。
下列矩阵中不能相似对角化的为( )。
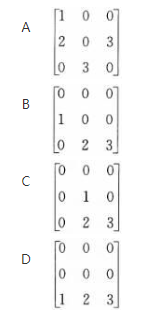

参考解析
解析:选项A中矩阵的特征值为1,3,-3,是3个单特征值,可相似对角化;选项C中矩阵的特征值为0,1,3,也是3个单特征值,可相似对角化;设选项D中的矩阵为D,则其特征值为0,0,3,且r(0E-D)=1,即3-r(0E-D)=2,故D可相似对角化。设选项B中的矩阵为B,则其特征值为0,0,3,且r(OE-B)=2,3-r(OE-B)-1≠2,故不可相似对角化。故选B。
相关考题:
设A,B为n阶矩阵,考虑以下命题:①若A,B为等价矩阵,则A,B的行向量组等价②若行列式.,则A,B为等价矩阵③若与都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则与的解空间的维数相同以上命题中正确的是( ).A.①③B.②④C.②③D.③④
单选题临界特质分析系统对工作进行挑选所采用的方法是()。A统计概率B特性参数C相似矩阵D职业矩阵