设f(x)具有二阶导数,y=f(x2),则的值是( )。A.f"(4)B.16f"(4)C.2f'(4)+16f"(4)D.2f'(4)+4f"(4)
设f(x)具有二阶导数,y=f(x2),则
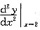
的值是( )。
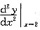
的值是( )。
A.f"(4)
B.16f"(4)
C.2f'(4)+16f"(4)
D.2f'(4)+4f"(4)
B.16f"(4)
C.2f'(4)+16f"(4)
D.2f'(4)+4f"(4)
参考解析
解析:利用复合函数求导法则求导后,再将x=2代入即得解
相关考题:
设函数f(x)具有二阶连续导数,且f(x)>0,f'(0)=0,则函数z=f(x)lnf(y)在点(0,0)处取得极小值的一个充分条件是 A.Af(0)>1,f"(0)>0B.f(0)>1,f"(0)C.f(0)0D.f(0)
设f(x)的二阶导数存在,且f′(x)=f(1-x),则下列式中何式可成立()?A、f″(x)+f′(x)=0B、f″(x)-f′(x)=0C、f″(x)+f(x)=0D、f″(x)-f(x)=0
若f″(x)存在,则函数y=ln[f(x)]的二阶导数为:()A、(f″(x)f(x)-[f′(x)]2)/[f(x)]2B、f″(x)/f′(x)C、(f″(x)f(x)+[f′(x)]2)/[f(x)]2D、ln″[f(x)]·f″(x)
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af″(x)+f(x)=0Bf′(x)+f(x)=0Cf″(x)+f′(x)=0Df″(x)+f′(x)+f(x)=0
单选题若f″(x)存在,则函数y=ln[f(x)]的二阶导数为:()A(f″(x)f(x)-[f′(x)]2)/[f(x)]2Bf″(x)/f′(x)C(f″(x)f(x)+[f′(x)]2)/[f(x)]2Dln″[f(x)]·f″(x)
单选题设f(x)的二阶导数存在,且f′(x)=f(1-x),则下列式中何式可成立()?Af″(x)+f′(x)=0Bf″(x)-f′(x)=0Cf″(x)+f(x)=0Df″(x)-f(x)=0
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af′(x)+f(x)=0Bf′(x)-f(x)=0Cf″(x)+f(x)=0Df″(x)-f(x)=0